第3話 大小比較はいかにしたら出来るか?
この大小比較は、
おそらく皆さんが予想しているより、
困難な課題です。
次の例のように、
25635
3208
桁数が違うなら、桁数の大きい方が大きい数です。
桁数を比較するには
n25635
n3208
終わりの印nまでの桁数を数えれば済みます。
ですが、桁数が同じときに、
大きな壁が現れます。
n1************
n2************
の例から、終わりの印nの1つ手前の数字を比較すれば、
大小が決するように見ます。
ところが、
n2************
n2************
のように、
最高位の数字だけを比較しただけでは大小が決定できない場合があります。
次の箱を開けて中身を確認しても、
n23************
n23************
左から2番目の位の数字も同じになってしまうケースもあります。
では、さらにもう1つ箱を開けて
n231***********
n234***********
なら大小が決まりますが、
n234***********
n234***********
となる可能性が残ります。
ならば、もうひとつの扉を開けて、
n2343**********
n2342**********
なら、大小決定ですが、
ここでも、
n2343**********
n2343**********
再び同じになる可能性があります。
ならば、一度10進数に直して比較する手がありそうですが、
987625070(16)=9×16の8乗+8×16の7乗+7×16の6乗+・・・
あたりで、簡単にlong longの範囲を超えてしまします。
n進数演算の究極の目的が、
巨大整数の研究である以上、
10進数に翻訳する方法は最初から不可能です。
ですから、パンドラの箱を開け続けるしかないのです。
n23431*********
n23431*********
n234310********
n234310********
n2343103*******
n2343103*******
ですが、どこまで行っても大小が決定できない場合もあります。
n23431031236987258
n23431031236987258
そうです。
同じ大きさの可能性があるのです。
桁数が同じ場合の大小比較は、
for文を使い、
終わりの印nの1つ手前から始めて、
大小が決定した段階で、
for文をbreak文によって強制的に抜ければよいのです。
では、ランダム2つのデータを発生させて、
大小を比較するプログラムを組んで下さい。
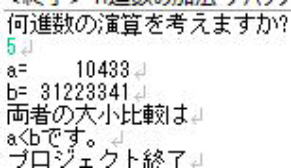
大小判定は、専用のchar型の関数
char ds(int* a,int* b,int n,int j1,int j2);
を用意して、
aの方が大きいときには2を返えし、
bの方が大きいときには0を返えし、
等しいときには1を返すようにして下さい。
そして、返された値を利用してmainで
a<b
等を表示して下さい。
