第7話 プログラム解説その1
プログラム主要部分再掲
int g(int* a,int* b,int* c,int n){
int i,j,k,d[10000],e[10000];
for(i=0;;i++){
if(a[i]==n){
j=i;
break;
}
}
for(i=0;;i++){
if(b[i]==n){
k=i;
break;
}
}
if(j>=k){
for(i=0;i<=j+2;i++){
c[i]=0;
d[i]=0;
e[i]=0;
}
for(i=0;i<j;i++)d[i]=a[i];
for(i=0;i<k;i++)e[i]=b[i];
for(i=0;i<j;i++){
c[i]+=(d[i]+e[i]);
c[i+1]+=c[i]/n;
c[i]=c[i]%n;
}
for(i=j+2;;i--){
if(c[i]>0){
c[i+1]=n;
return(i+1);
}
}
}
else{
for(i=0;i<=k+2;i++){
c[i]=0;
d[i]=0;
e[i]=0;
}
for(i=0;i<k;i++)d[i]=b[i];
for(i=0;i<j;i++)e[i]=a[i];
for(i=0;i<k;i++){
c[i]+=(d[i]+e[i]);
c[i+1]+=c[i]/n;
c[i]=c[i]%n;
}
for(i=k+2;;i--){
if(c[i]>0){
c[i+1]=n;
return(i+1);
}
}
}
}
プログラム解説
for(i=0;;i++){
if(a[i]==n){
j=i;
break;
}
}
for(i=0;;i++){
if(b[i]==n){
k=i;
break;
}
}
では、終わりの印nを探索しています。
if(j>=k){
・・・
}
else{
・・・
}
となっているのは、a[i]とb[i]の桁数がどちらが大きいのか、
で場合分けをしています。
すなわち、
a[i]≧b[i]
と
a[i]<b[i]
のそれぞれの場合で処理をしています。
a[i]の桁数がb[i]の桁数以上の場合には、
if(j>=k){
for(i=0;i<=j+2;i++){
c[i]=0;
d[i]=0;
e[i]=0;
}
初期化は、a[i]の桁数であるjまでで十分ですが、
念のため少し大きめに初期化をしています。
足し算で、桁数が増える可能性を考えているわけです。
といっても足し算で二桁増える可能性はないので、
if(j>=k){
for(i=0;i<=j+1;i++){
c[i]=0;
d[i]=0;
e[i]=0;
}
か
if(j>=k){
for(i=0;i<=j;i++){
c[i]=0;
d[i]=0;
e[i]=0;
}
でも十分だとは思われますが、
まさに念のためです。
次の行の
for(i=0;i<j;i++)d[i]=a[i];
for(i=0;i<k;i++)e[i]=b[i];
は大きい方をd[i]に、
小さい方をe[i]に代入しています。
5進数で例えば、
a[i]とb[i]がそれぞれ、
54023
5214
すなわち、
a[0]=3,a[1]=2,a[2]=0,a[3]=4,a[4]=5
b[0]=4,b[1]=1,b[2]=2,b[3]=5
(逆順になっていることに注意してください。)
であったとしますと、d[i]とe[i]はそれぞれ
04023
00214
すなわち、
d[0]=3,d[1]=2,d[2]=0,d[3]=4,d[4]=0
e[0]=4,e[1]=1,e[2]=2,e[3]=0,e[4]=0
となります。これであれば、

となって上手く計算できます。
もしこれが、
54023
5214
のままであったとすると、
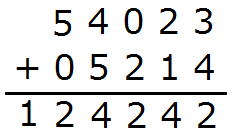
とおかしなことになってしまいます。
終わりの記号n(この例だと5)は、
表示のときには便利ですが、
四則演算(加減乗除)するときには、
邪魔をするのです。
なので、一端その終わり記号nを外す作業が必要になります。
