第20講 末項確定法による魔方陣自動生成ソフトの高速化
第1話 末項確定法とは?
今回も
初心者のための VC++ 入門 (C++ 入門) 講義 基礎から応用まで(第3部)
第21講第1話末項確定法とは?
から、引用させて頂きます。
---以下引用---
今回はいつもと手法を変えて、
最初に、今回の成果を最初に紹介した後に、
末項確定法とは何か説明しましょう。
以下のデータは各次魔方陣を100個作るのにかかった時間です。
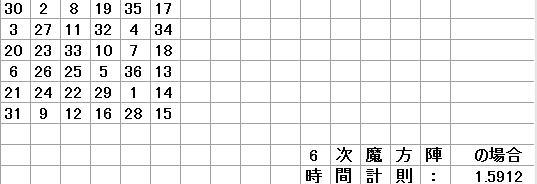
1個あたり0.015912秒です。
前話のデータが0.07284秒ですから、約4.6倍のスピード差です。
さらに、10次魔方陣の場合
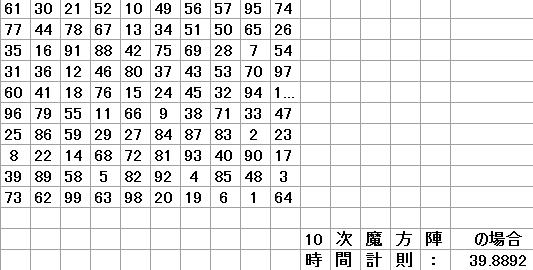
1個あたり0.398892秒ですから、約5.6倍です。
今までソフトがバージョンアップする度に、
1万倍とか1100万倍とかとう桁外れの性能アップを見せていたのに比べるとかなり地味に見えるかもしれませんが、
結構大きな戦果だと思います。
プログラミングの世界では、1.1倍でも大きな成果です。
(例えば、数独問題作成ソフトのスピードを1.1倍にするのに私は数日も場合によっては数週間費やしていました。
皆さんからすれば結果だけ見ているので、その苦労は見えないと思いますが、
プログラミングとは地味な研究の積み重ねなのです。
ただ、前々話で紹介したようにときには驚愕の成果を見せることもあります。)
ですから5,6倍はかなり大きな成果です。
さらに、今回の改良によって11次魔方陣も1個あたり約0.056秒でできています。
前話のときは途中で実験を打ち切ってしまったので、単純比較はできませんが、
20秒まで探索範囲を広げて、60分も実験を続けましたが最適乱数系列を発見できませんでしたので、
仮に前話のソフトが20秒であると前提しても、
20÷0.056=約360倍です。
| y |
|
|
|
|
|
|
|
|
|
|
|
|
| ↓ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
← |
x |
| 0 |
0 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
10 |
|
|
| 1 |
28 |
1 |
36 |
37 |
38 |
39 |
40 |
41 |
11 |
42 |
|
|
| 2 |
29 |
43 |
2 |
50 |
51 |
52 |
53 |
12 |
54 |
55 |
|
|
| 3 |
30 |
44 |
56 |
3 |
62 |
63 |
13 |
64 |
65 |
66 |
|
|
| 4 |
31 |
45 |
57 |
67 |
4 |
14 |
72 |
73 |
74 |
75 |
|
|
| 5 |
32 |
46 |
58 |
68 |
15 |
5 |
80 |
81 |
82 |
83 |
|
|
| 6 |
33 |
47 |
59 |
16 |
76 |
84 |
6 |
88 |
89 |
90 |
|
|
| 7 |
34 |
48 |
17 |
69 |
77 |
85 |
91 |
7 |
94 |
95 |
|
|
| 8 |
35 |
18 |
60 |
70 |
78 |
86 |
92 |
96 |
8 |
98 |
|
|
| 9 |
19 |
49 |
61 |
71 |
79 |
87 |
93 |
97 |
99 |
9 |
|
|
末講確定法とは、水色以外のセルについては、初めから入る数字は確定していることに、
着眼した方法です。
例えば、
| y |
|
|
|
|
|
|
|
|
|
|
|
|
| ↓ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
← |
x |
| 0 |
0 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
10 |
|
|
| 1 |
28 |
1 |
36 |
37 |
38 |
39 |
40 |
41 |
11 |
42 |
|
|
| 2 |
29 |
43 |
2 |
50 |
51 |
52 |
53 |
12 |
54 |
55 |
|
|
| 3 |
30 |
44 |
56 |
3 |
62 |
63 |
13 |
64 |
65 |
66 |
|
|
| 4 |
31 |
45 |
57 |
67 |
4 |
14 |
72 |
73 |
74 |
75 |
|
|
| 5 |
32 |
46 |
58 |
68 |
15 |
5 |
80 |
81 |
82 |
83 |
|
|
| 6 |
33 |
47 |
59 |
16 |
76 |
84 |
6 |
88 |
89 |
90 |
|
|
| 7 |
34 |
48 |
17 |
69 |
77 |
85 |
91 |
7 |
94 |
95 |
|
|
| 8 |
35 |
18 |
60 |
70 |
78 |
86 |
92 |
96 |
8 |
98 |
|
|
| 9 |
19 |
49 |
61 |
71 |
79 |
87 |
93 |
97 |
99 |
|
|
|
と来たときに、青のセルに入る数字は決まっています。
| 6 |
2 |
2 |
5 |
0 |
4 |
5 |
5 |
9 |
7 |
| 7 |
4 |
7 |
6 |
1 |
3 |
5 |
4 |
6 |
2 |
| 3 |
1 |
9 |
8 |
4 |
7 |
6 |
2 |
0 |
5 |
| 3 |
3 |
1 |
4 |
7 |
3 |
4 |
5 |
6 |
9 |
| 5 |
4 |
1 |
7 |
1 |
2 |
4 |
3 |
9 |
9 |
| 9 |
7 |
5 |
1 |
6 |
0 |
3 |
7 |
3 |
4 |
| 2 |
8 |
5 |
2 |
2 |
8 |
8 |
8 |
0 |
2 |
| 0 |
2 |
1 |
6 |
7 |
8 |
9 |
3 |
8 |
1 |
| 3 |
8 |
5 |
0 |
8 |
9 |
0 |
8 |
4 |
0 |
| 7 |
6 |
9 |
6 |
9 |
1 |
1 |
0 |
0 |
6 |
(表を見るときには、セルに入っている数字がセル番号のgかそのセルに実際に入っている数字かを常に区別してください。
上表の数字は、セル番号gではなく、そのセルに入っている実際の数字です。
本講義においては、セル番号gのときは基本的にはピンクとしています。)
6+4+9+4+1+0+8+3+4=39
対角線の合計は、
0+1+2+3+4+5+6+7+8+9=45
ですから、
に入る数字は
45-39=6
と確定してしまうのです。
ですから、このセルについてはfor文で探索するのは無駄です。
に来たら、for文は通らないで次の世界(g+1)に進むか、
前の世界(g-1)に戻るしかないのです。
戻る場合の言うのは、例えば
| 6 |
2 |
2 |
5 |
0 |
4 |
5 |
5 |
9 |
7 |
| 7 |
4 |
7 |
6 |
1 |
3 |
5 |
4 |
6 |
2 |
| 3 |
1 |
9 |
8 |
4 |
7 |
6 |
2 |
0 |
5 |
| 3 |
3 |
1 |
4 |
7 |
3 |
4 |
5 |
6 |
9 |
| 5 |
4 |
1 |
7 |
1 |
2 |
4 |
3 |
9 |
9 |
| 9 |
7 |
5 |
1 |
6 |
0 |
3 |
7 |
3 |
4 |
| 2 |
8 |
5 |
2 |
2 |
8 |
8 |
8 |
0 |
2 |
| 0 |
2 |
1 |
6 |
7 |
8 |
9 |
0 |
8 |
1 |
| 3 |
8 |
5 |
0 |
8 |
9 |
0 |
8 |
2 |
0 |
| 7 |
6 |
9 |
6 |
9 |
1 |
1 |
0 |
0 |
6 |
なら、6+4+9+4+1+0+8+0+2=34ですが、
合計の45との差をとると、45-34=11
にはいる最大数は9ですから、
このセルのある対角線の合計を45にするのは不可能になっているわけです。
この場合には1つ前のセル
に戻ってやり直すしかありません。
あるいは
| 6 |
2 |
2 |
5 |
0 |
4 |
5 |
5 |
9 |
7 |
| 7 |
4 |
7 |
6 |
1 |
3 |
5 |
4 |
6 |
2 |
| 3 |
1 |
9 |
8 |
4 |
7 |
6 |
2 |
0 |
5 |
| 3 |
3 |
1 |
4 |
7 |
3 |
4 |
5 |
6 |
9 |
| 5 |
4 |
1 |
7 |
1 |
2 |
4 |
3 |
9 |
9 |
| 9 |
7 |
5 |
1 |
6 |
2 |
3 |
7 |
3 |
4 |
| 2 |
8 |
5 |
2 |
2 |
8 |
8 |
8 |
0 |
2 |
| 0 |
2 |
1 |
6 |
7 |
8 |
9 |
5 |
8 |
1 |
| 3 |
8 |
5 |
0 |
8 |
9 |
0 |
8 |
7 |
0 |
| 7 |
6 |
9 |
6 |
9 |
1 |
1 |
0 |
0 |
6 |
の場合も6+4+9+4+1+2+8+5+7=46となり、
に入る数字が-1となってしまいこれも禁則に反します。
セルに入る数字は0から9までですから。
この場合にも
に戻ってやり直すしかありません。
---以上引用---
末項確定法とは、
一番最後の項(セル)は決まっていることに着目する
魔方陣自動生成方法です。
確定できるセルは、
| y |
|
|
|
|
|
|
|
|
|
|
|
|
| ↓ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
← |
x |
| 0 |
0 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
10 |
|
|
| 1 |
28 |
1 |
36 |
37 |
38 |
39 |
40 |
41 |
11 |
42 |
|
|
| 2 |
29 |
43 |
2 |
50 |
51 |
52 |
53 |
12 |
54 |
55 |
|
|
| 3 |
30 |
44 |
56 |
3 |
62 |
63 |
13 |
64 |
65 |
66 |
|
|
| 4 |
31 |
45 |
57 |
67 |
4 |
14 |
72 |
73 |
74 |
75 |
|
|
| 5 |
32 |
46 |
58 |
68 |
15 |
5 |
80 |
81 |
82 |
83 |
|
|
| 6 |
33 |
47 |
59 |
16 |
76 |
84 |
6 |
88 |
89 |
90 |
|
|
| 7 |
34 |
48 |
17 |
69 |
77 |
85 |
91 |
7 |
94 |
95 |
|
|
| 8 |
35 |
18 |
60 |
70 |
78 |
86 |
92 |
96 |
8 |
98 |
|
|
| 9 |
19 |
49 |
61 |
71 |
79 |
87 |
93 |
97 |
99 |
9 |
|
|
少なくとも、20カ所に上ります。
皆さん、
前講で作った対角線法魔方陣自動生成ソフト
#include<iostream>
#include <time.h>
using namespace std;
long f(int *k,int **x,int n,long cn,int g,int *p,int *q);
void ts(int **x,int n,int *p,int *q);
void h(int **x,int n);
void syokika(int n,int *k);
void zh(int n,int *p,int *q);
void main(){
int n;
cout<<"何次魔方陣を生成しますか?"<<endl;
scanf("%d",&n);
int **x=(int **)malloc(sizeof(int)*n);
for(char i=0;i<n;i++)x[i]=(int *)malloc(sizeof(int)*n);
int *k=(int *)malloc(sizeof(int)*n*n);
int p[100],q[100];
cout<<endl;
clock_t hj,ow; //clock_t型の宣言、プログラム開始時間を取得するための変数
hj=clock();
syokika(n,k);
zh(n,p,q);
//ts(x,n,p,q);
//cout<<n<<"次魔方陣が"<<f(k,x,n,0,0)<<"個生成されました。"<<endl;
ow=clock();
cout<<"魔方陣生成にかかった時間は"<<(double)(ow-hj)/1000<<"秒です。"<<endl;
}
void ts(int **x,int n,int *p,int *q){
int i,j;
for(i=0;i<n*n;i++)x[q[i]][p[i]]=i;
for(i=0;i<n;i++){
for(j=0;j<n;j++){
if(x[i][j]<10)cout<<"0"<<x[i][j]<<"
"; else cout<<x[i][j]<<" ";
}
cout<<endl;
}
}
void zh(int n,int *p,int *q){
int i,j,cn;
int a[10][10];
for(i=0;i<n;i++)
for(j=0;j<n;j++)
a[i][j]=-1;
for(i=0;i<n;i++)a[i][i]=i;
cn=n;
for(i=0;i<n;i++){
if(a[i][n-1-i]==-1){
a[i][n-1-i]=cn;
cn++;
}
}
for(i=0;i<n;i++){
for(j=0;j<n;j++){
if(a[i][j]==-1){
a[i][j]=cn;
cn++;
}
}
}
for(i=0;i<n;i++){
for(j=0;j<n;j++){
p[a[i][j]]=j;
q[a[i][j]]=i;
}
}
}
void syokika(int n,int *k){
for(int i=0;i<n*n;i++)k[i]=0;
}
long f(int *k,int **x,int n,long cn,int g,int *p,int *q){
int i,j,s,t,w,v;
s=q[g];
t=p[g];
int ii,iii;
if(n==5)srand(14);
ii=rand()%(n*n);
for(iii=1;iii<n*n+1;iii++){
i=(iii+ii)%(n*n)+1;
x[s][t]=i;
v=0;
if(k[i-1]==0){
k[i-1]=1;
v=1;
}
else{
goto tobi;
}
if(s==n-1 && t==n-1){
w=0;
for(j=0;j<n;j++)w=w+x[j][j];
if(w!=n*(n*n+1)/2)goto tobi;
}
if(s==n-1 && t==0){
w=0;
for(j=0;j<n;j++)w=w+x[j][n-1-j];
if(w!=n*(n*n+1)/2)goto tobi;
}
if(s==0 && t==n-2){
w=0;
for(j=0;j<n;j++)w+=x[s][j];
if(w!=n*(n*n+1)/2)goto tobi;
}
for(j=0;j<n;j++)w+=x[j][t];
if(w!=n*(n*n+1)/2)goto tobi;
}
if(s>0 && s<n-1 && t==n-1){
w=0;
for(j=0;j<n;j++)w+=x[s][j];
if(w!=n*(n*n+1)/2)goto tobi;
}
if(s==n-1 && t>0 && t<n-1){
w=0;
for(j=0;j<n;j++)w+=x[j][t];
if(w!=n*(n*n+1)/2)goto tobi;
}
if(g+1<n*n){
cn=f(x,n,cn,g+1);
if(cn==100)return(cn);
}
else{
h(x,n);
cn++;
if(cn==100)return(cn);
}
tobi:;
if(cn==100)return(cn);
if(v==1)k[i-1]=0;
}
return(cn);
}
void h(int **x,int n){
for(char i=0;i<n;i++){
for(char j=0;j<n;j++){
if(n==3)cout<<x[i][j]<<" ";
if(n>3)if(x[i][j]<10)cout<<"0"<<x[i][j]<<"
"; else cout<<x[i][j]<<" ";
}
cout<<endl;
}
cout<<endl;
}
参考ダウンロードファイル
を改良していきましょう。
といっても、ここまでついていらっしゃった優秀な皆さんでも、
いきなりすべてご自分で行うのは、大変ですから、
私と一緒に少しずつ改良していきましょう。
まず、対角線部分の改良から。
尚、改良効果を調べるために乱数は外して、
long f(int **x,int n,long cn,int g){
int i,j,s,t,w,v;
s=g/n;
t=g%n;
for(i=1;i<n*n+1;i++){
x[s][t]=i;
に戻しておきましょう。
第18講第8話へ 第2話へ

eclipse c++ 入門講義第1部へ
魔方陣 数独で学ぶ VBA 入門
数独のシンプルな解き方・簡単な解法の研究
VB講義へ
VB講義基礎へ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座
初心者のための世界で一番わかりやすいVBA入門講義(基礎から応用まで)
初心者のための VC++による C言語 C++ 入門 基礎から応用まで第1部
eclipse java 入門
java 入門 サイト 基礎から応用まで
VC++ C言語 C++ 入門 初心者 基礎から応用まで
本サイトトップへ


