第８講 for文・if文・配列・ポインタを総動員して３次魔方陣の自動生成に挑戦する！
第３話 ３次順列作成プログラムに総数カウントを付け加える

総数カウントプログラム例
#include<iostream>
using namespace std;
int f(int *x,int cn);
void g(int *x);
void main(){
　　 int x[3];
　　 int y;
　　 y=f(x,0);
　　 cout<<endl<<"3次順列総数は"<<y<<endl;
}
int f(int *x,int cn){
　　 int i,j,k,l;
　　 for(i=1;i<4;i++){
　　　　　x[0]=i;
　　　　　for(j=1;j<4;j++){
　　　　　　　 x[1]=j;
　　　　　　　 if(x[1]!=x[0]){
　　　　　　　　　　for(k=1;k<4;k++){
　　　　　　　　　　　　 x[2]=k;
　　　　　　　　　　　　 if(x[2]!=x[0] && x[2]!=x[1]){
　　　　　　　　　　　　　　　g(x);
　　　　　　　　　　　　　　　cn++;
　　　　　　　　　　　　 }
　　　　　　　　　　}
　　　　　　　 }
　　　　　}
　　 }
　　 return(cn);
}

void g(int *x){
　　 for(int i=0;i<3;i++)cout<<x[i]<<" ";
　　 cout<<endl;
}

さて、次に４次、５次、６次、・・・と考えていきますが、
次数が進みに従いまして、
x[4]!=x[0] && x[4]!=x[1] && x[4]!=x[2] && x[4]!=x[3]
などと条件式が長くなってしまいます。
そこで、４次以降の順列を考えるために、
関数fのコードを次のように変更しておきます。
int f(int *x,int cn){
　　 int i,j,k;
　　 for(i=1;i<4;i++){
　　　　　x[0]=i;
　　　　　for(j=1;j<4;j++){
　　　　　　　 x[1]=j;
　　　　　　　 if(x[1]==x[0])goto tobi1;
　　　　　　　 for(k=1;k<4;k++){
　　　　　　　　　　x[2]=k;
　　　　　　　　　　if(x[2]==x[0] || x[2]==x[1])goto tobi2;
　　　　　　　　　　g(x);
　　　　　　　　　　cn++;
　　　　　　　 　　 tobi2:;
　　　　　　　 }
　　　　　　　 tobi1:;
　　　　　}
　　 }
　　 return(cn);
}

　　　　　　　 if(x[1]==x[0])goto tobi1;
や
　　　　　　　　　　　　 if(x[2]==x[0] || x[2]==x[1])goto tobi2;
はgoto文と呼ばれるもので、
BASICの時代スパゲティプログラムの元凶、
構造化プログラミング＝わかりやすいプログラミングを妨げるものとして、
大変評判が悪かったものですが、
出口と入り口を１つに決めておけば、
私は、問題ないと思います。
あっちに行ったりこっちに行ったりしなければよいということです。
流れが直線的なら、わかりやすいの原則に反しないからです。
　　　　　　　 if(x[1]==x[0])goto tobi1;
はx[0]==x[1]が成立するときは、tobi1に飛びなさいという命令です。
つまり、このときは
　　　　　　　 for(k=1;k<4;k++){
　　　　　　　　　　x[2]=k;
　　　　　　　　　　if(x[2]==x[0] || x[2]==x[1])goto tobi2;
　　　　　　　　　　g(x);
　　　　　　　　　　cn++;
　　　　　　　 　　 tobi2:;
　　　　　　　 }
が一切実行されないのです。
尚、x[2]==x[0] || x[2]==x[1]はx[2]==x[0]またはx[2]==x[1]という意味です。
||が『または』を意味するわけです。

一般に、条件
ｐかつｑの否定は
（ｐでない）または（ｑでない）
となります。
また、ｐまたはｑ
の否定は、
（ｐでない）かつ（ｑでない）
になります。

「かつ」という言葉に聞き慣れていない人もいると思いますが、
ｐかつｑ
は条件ｐも条件ｑも同時に満たすことを表します。

それに対して、
ｐまたはｑ
は条件ｐを満たすか、条件ｑを満たしていればよいのです。
どちらか一方の条件を満たしていればよいのですから、
両方の条件を満たすｐかつｑの状態でもいいのです。

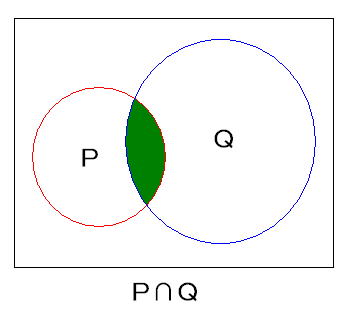
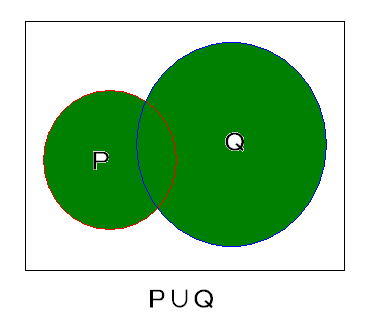
集合の図を書いてみましょう。
条件ｐを満たす集合をＰ、
条件ｑを満たす集合をＱ、
ｐかつｑを満たす集合をＰ∩Ｑ、
ｐまたはｑを満たす集合をＰ∪Ｑと表すことにしますと、
下図のようになります。


したがって、条件ｐまたはｑの否定を表す集合は、

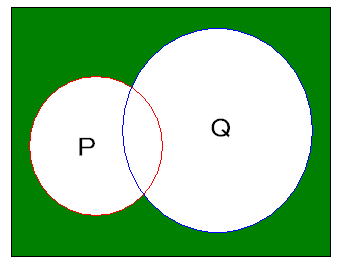
となり、条件ｐまたはｑの否定は（ｐでない）かつ（ｑでない）となります。
また、条件ｐかつｑの否定を表す集合は、

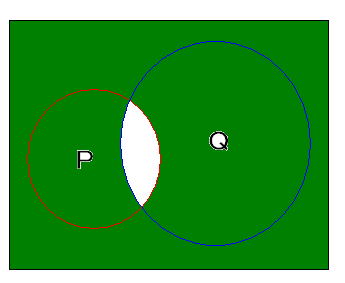
となり、条件ｐかつｑの否定は（ｐでない）または（ｑでない）になります。

さらに、
　　　　　　　　　　if(x[2]==x[0] || x[2]==x[1])goto tobi2;
　　　　　　　　　　g(x);
　　　　　　　　　　n++;
　　　　　　　 　　 tobi2:;
の部分は、
　　　　　　　　　　if(x[2]==x[0])goto tobi2;
　　　　　　　　　　if(x[2]==x[1])goto tobi2;
　　　　　　　　　　g(x);
　　　　　　　　　　n++;
　　　　　　　 　　 tobi2:;
とすることもできます。
これを４次以降のヒントとします。

第２話へ　第４話へ



魔方陣 数独で学ぶ VBA 入門
数独のシンプルな解き方・簡単な解法の研究
VB講義へ
ＶＢ講義基礎へ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座
初心者のための世界で一番わかりやすいVBA入門講義（基礎から応用まで）
初心者のための VC++による C言語 C++ 入門 基礎から応用まで第１部
eclipse java 入門
java 入門 サイト 基礎から応用まで
VC++ C言語 C++ 入門 初心者 基礎から応用まで
本サイトトップへ