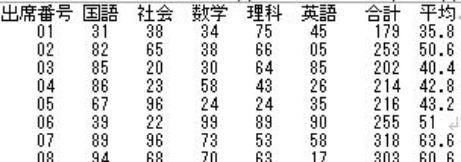
を実現するプログラム例
#include <iomanip>
using namespace std;
int x[40][6];
int sg[40];
float sh[40];
void f1(); //1行目(ラベル)表示
void f2(); //データ作成
void f3(); //データ表示と各生徒合計・平均の表示
void f4(); //各教科の合計と平均を算出して表示
void f5(); //各生徒の合計と平均の算出
void main(){
f1(); //1行目(ラベル)表示
f2(); //データ作成
f5(); //各生徒の合計と平均の算出
f3(); //データ表示と各生徒合計・平均の表示
f4(); //各教科の合計と平均を算出して表示
}
//1行目(ラベル)表示
void f1(){
cout<<"出席番号 国語 社会 数学 理科 英語"<<endl;
}
//データ作成
void f2(){
srand(time(NULL));
int i,j;
for(i=0;i<40;i++)x[i][0]=i+1;
for(i=0;i<40;i++){
for(j=1;j<6;j++){
x[i][j]=rand()%100;
}
}
}
//データ表示と各生徒合計・平均の表示
void f3(){
int i,j;
for(i=0;i<40;i++){
for(j=0;j<6;j++){
if(j==0)cout<<" ";
if(x[i][j]<10)cout<<"0"<<x[i][j]<<" ";
if(x[i][j]>=10)cout<<x[i][j]<<" ";
}
cout<<" "<<sg[i]<<" "<<setprecision(3)<<sh[i]<<" ";
cout<<endl;
}
cout<<endl;
}
//各教科の合計と平均を算出して表示
void f4(){
int w[5]; //各教科の合計を入れる配列
float h[5]; //各教科の平均を入れる配列
int i,j;
for(i=0;i<5;i++)w[i]=0;
for(i=0;i<5;i++){
for(j=0;j<40;j++){
w[i]=w[i]+x[i][j];
}
h[i]=(float)w[i]/40;
}
cout<<"合計 ";
for(i=0;i<5;i++)cout<<w[i]<<" ";
cout<<endl;
cout<<"平均 ";
for(i=0;i<5;i++)cout<<setprecision(4)<<h[i]<<" ";
cout<<endl;
}
//各生徒の合計と平均の算出
void f5(){
int i,j;
for(i=0;i<40;i++)sg[i]=0; //各生徒合計の初期化
for(i=0;i<40;i++){
for(j=0;j<5;j++){
sg[i]=sg[i]+x[j][i+1];
}
sh[i]=(float)sg[i]/5;
}
}
2次元配列とfor文を組み合わせれば、
3次魔方陣自動生成プログラムを組むことができるなど、
配列を使った面白いプログラムはたくさん組むことができますが、
3次魔方陣自動生成プログラムなどの興味深いテーマは、
独立の講にしたいと思います。
尚、魔方陣とは
