第７講 多次元配列と1次元配列の関係
第２話 第６講第３話の課題を1次元配列で実現する

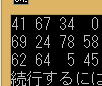
を１次元配列
　　　　　　int[] a = new int[12];
によって実現するコード例
//以下C#を始めるためのお呪い
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
//以上C#を始めるためのお呪い
namespace a //初心者はお呪い＝決まり事と思い一切気にしない
{
　　class Program //初心者はお呪い＝決まり事と思い一切気にしない
　　{
　　　　static void Main[string[] args] //私は社長だ。
　　　　{
　　　　　　f[];
　　　　}
　　　　static void f[]
　　　　{
　　　　　　int[] a = new int[12];
　　　　　　Random r = new Random[];
　　　　　　//以下データ生成
　　　　　　for [int i = 0; i < 3; i++]
　　　　　　{
　　　　　　　　for [int j = 0; j < 4; j++]
　　　　　　　　{
　　　　　　　　　　a[4 * i + j] = r.Next[100];
　　　　　　　　}
　　　　　　}
　　　　　　//以下データ表示
　　　　　　for [int i = 0; i < 3; i++]
　　　　　　{
　　　　　　　　for [int j = 0; j < 4; j++]
　　　　　　　　{
　　　　　　　　　　if [a[4 * i + j] < 10] Console.Write[" {0:d} ", a[4 * i + j]]; //１桁の場合
　　　　　　　　　　if [a[4 * i + j] >= 10] Console.Write["{0:d} ", a[4 * i + j]]; //２桁の場合
　　　　　　　　}
　　　　　　　　Console.WriteLine[];
　　　　　　}
　　　　}
　　}
}


解説
今回の課題は２次元配列a[3, 4]と１次元配列a[12]とをいかに対応させるかです。
すなわち、（以下色を対応させています!）
a[0, 0],a[0, 1],a[0, 2],a[0, 3],a[1, 0],a[1, 1],a[1, 2],a[1, 3],a[2, 0],a[2, 1],a[2, 2],a[2, 3]
a[0],　　 a[1],　 a[2],　 a[3],　　a[4],　 a[5],　 a[6],　 a[7],　　a[8],　 a[9],　 a[10],　a[11]
の対応関係をいかにするかです。

（0の色が１次元配列の添え字）
jの0の列に注目すると、0,4,8です。
そのほかの列も
1,5,9
2,6,10
3,7,11
と4ずつ増えています。
これはjが
0,1,2,3,4
と４つの場合をとるからです。
すなわち4飛びにすれば良いので、
4 * i + j
です。

では、第６講第４話の課題

を１次元配列によって、実現して下さい。
ただし、データ生成とデータ表示はすべて１次元for文で行うものとします。