第4話 もとの行列・左右反転行列・上下反転行列・転置行列のすべてを表示する
実行画面
行列
1 7 4 0 9 4 8
8 2 4 5 5 1 7
1 1 5 2 7 6 1
4 2 3 2 2 1 6
8 5 7 6 1 8 9
2 7 9 5 4 3 1
左右反転行列
8 4 9 0 4 7 1
7 1 5 5 4 2 8
1 6 7 2 5 1 1
6 1 2 2 3 2 4
9 8 1 6 7 5 8
1 3 4 5 9 7 2
上下反転行列
2 7 9 5 4 3 1
8 5 7 6 1 8 9
4 2 3 2 2 1 6
1 1 5 2 7 6 1
8 2 4 5 5 1 7
1 7 4 0 9 4 8
転置行列
1 8 1 4 8 2
7 2 1 2 5 7
4 4 5 3 7 9
0 5 2 2 6 5
9 5 7 2 1 4
4 1 6 1 8 3
8 7 1 6 9 1
を実現するプログラム例
#include<iostream> //入出力のために組み込む
using namespace std; //coutを使えるようにするために必要
void f(int **x); //データ作成
void g(int **x); //行列表示
void h(int **x); //左右反転行列表示
void s(int **x); //上限反転行列表示
void t(int **x); //転置行列表示
int main() {
int **a = (int **)malloc(sizeof(int *) * 6), i; //配列の宣言
for (i = 0; i < 10; i++)a[i] = (int *)malloc(sizeof(int) * 7);
//行列のデータ入力
f(a);
//行列の表示
g(a);
//左右反転行列の表示
h(a);
//上限反転行列の表示
s(a);
//転置行列の表示
t(a);
}
void f(int **x) {
int i, j;
//配列のデータ作成
for (i = 0; i < 6; i++) {
for (j = 0; j < 7; j++)x[i][j] = rand() % 10;
}
}
void g(int **x) {
int i, j;
//配列のデータ
cout << "行列" << endl;
for (i = 0; i < 6; i++) {
for (j = 0; j < 7; j++)cout << x[i][j] << " ";
cout << endl; //改行
}
cout << endl; //改行
}
void h(int **x) {
int i, j;
//配列のデータ表示
cout << "左右反転行列" << endl;
for (i = 0; i < 6; i++) {
for (j = 0; j < 7; j++)cout << x[i][6 - j] << " ";
cout << endl; //改行
}
cout << endl; //改行
}void s(int **x) {
int i, j;
//配列のデータ表示
cout << "上下反転行列" << endl;
for (i = 0; i < 6; i++) {
for (j = 0; j < 7; j++)cout << x[5 - i][j] << " ";
cout << endl; //改行
}
cout << endl; //改行
}void t(int **x) {
int i, j;
//配列のデータ表示
cout << "転置行列" << endl;
for (i = 0; i < 7; i++) {
for (j = 0; j < 6; j++)cout << x[j][i] << " ";
cout << endl; //改行
}
cout << endl; //改行
}
さて、main()で配列(実際にはポインタ)を作り渡していましたが、
関数側から配列を戻すことが出来るでしょうか。
つまり、戻り値を配列にすることは出来るでしょうか。
もちろん配列を戻り値にすることは出来ません。
関数のところで言い忘れましたが、
関数は必ず1つの値のみを返します。
ですから、C言語の関数も戻す値は1つです。
ならば、配列を社長以外の社員が作り、
社長に返すことができかといいますと、
出来るが答えです。
下の図では、配列の先頭アドレスである
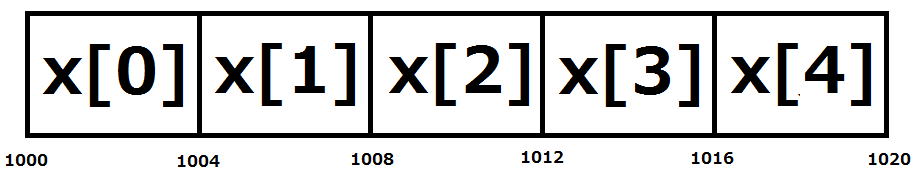
1000を社員から返してもらえれば、
社長はx[0]からx[4]までのデータを受け取ることが出来ます。
連続する番地に5つのデータが入っているからです。
関数は1つの値しか返せませんが、
1000という配列のアドレス(正確には1つ手前のアドレス)を受け取れば、
1001〜1004、1005〜1008、1009〜10012、1013〜1016、1017〜1020
に入っているデータを引き出すことが出来ます。
実質配列を返してもらったのと同じ結果になります。
では、これを確認するコードを考えて下さい。
ただし、実行画面は
行列
1 7 4 0 9 4 8
8 2 4 5 5 1 7
1 1 5 2 7 6 1
4 2 3 2 2 1 6
8 5 7 6 1 8 9
2 7 9 5 4 3 1
左右反転行列
8 4 9 0 4 7 1
7 1 5 5 4 2 8
1 6 7 2 5 1 1
6 1 2 2 3 2 4
9 8 1 6 7 5 8
1 3 4 5 9 7 2
上下反転行列
2 7 9 5 4 3 1
8 5 7 6 1 8 9
4 2 3 2 2 1 6
1 1 5 2 7 6 1
8 2 4 5 5 1 7
1 7 4 0 9 4 8
転置行列
1 8 1 4 8 2
7 2 1 2 5 7
4 4 5 3 7 9
0 5 2 2 6 5
9 5 7 2 1 4
4 1 6 1 8 3
8 7 1 6 9 1
であるとします。
