第2話 For文の入れ子式利用による2次元ループ解答例

を実現するコード例
Private Sub CommandButton1_Click()
Dim i As Byte, j As Byte
For i = 1 To 10
For j = 1 To 10
Cells(4 + i, 1 + j) = "○"
Next
Next
End Sub
参考ファイル
解説
簡単にトレースしてみましょう。
i = 1 の場合
j = 1 のとき
Cells(4 + i, 1 + j) = "○"
は
Cells(4 + 1, 1 + 1) = "○"
から
Cells(5, 2) = "○"
で確かにB5に○が入ります。
j = 2 のとき
Cells(4 + i, 1 + j) = "○"
は
Cells(4 + 1, 1 + 2) = "○"
から
Cells(5, 3) = "○"
で確かにC5に○が入ります。
j = 3 のとき
Cells(4 + i, 1 + j) = "○"
は
Cells(4 + 1, 1 + 3) = "○"
から
Cells(5, 4) = "○"
で確かにD5に○が入ります。
・
・
・
j = 10 のとき
Cells(4 + i, 1 + j) = "○"
は
Cells(4 + 1, 1 + 10) = "○"
から
Cells(5, 11) = "○"
で確かにK5に○が入ります。
i = 2 の場合
j = 1 のとき
Cells(4 + i, 1 + j) = "○"
は
Cells(4 + 2, 1 + 1) = "○"
から
Cells(6, 2) = "○"
で確かにB6に○が入ります。
j = 2 のとき
Cells(4 + i, 1 + j) = "○"
は
Cells(4 + 2, 1 + 2) = "○"
から
Cells(6, 3) = "○"
で確かにC6に○が入ります。
・
・
・
j = 10 のとき
Cells(4 + i, 1 + j) = "○"
は
Cells(4 + 2, 1 + 10) = "○"
から
Cells(6, 11) = "○"
で確かにK6に○が入ります。
・
・
・
i = 10 の場合
j = 1 のとき
Cells(4 + i, 1 + j) = "○"
は
Cells(4 + 10, 1 + 1) = "○"
から
Cells(14, 2) = "○"
で確かにB14に○が入ります。
j = 2 のとき
Cells(4 + i, 1 + j) = "○"
は
Cells(4 + 10, 1 + 2) = "○"
から
Cells(14, 3) = "○"
で確かにC14に○が入ります。
・
・
・
j = 10 のとき
Cells(4 + i, 1 + j) = "○"
は
Cells(4 + 10, 1 + 10) = "○"
から
Cells(14, 11) = "○"
で確かにK14に○が入ります。
以上から、

となります。
では次の課題です。
実行ボタンを押すと、
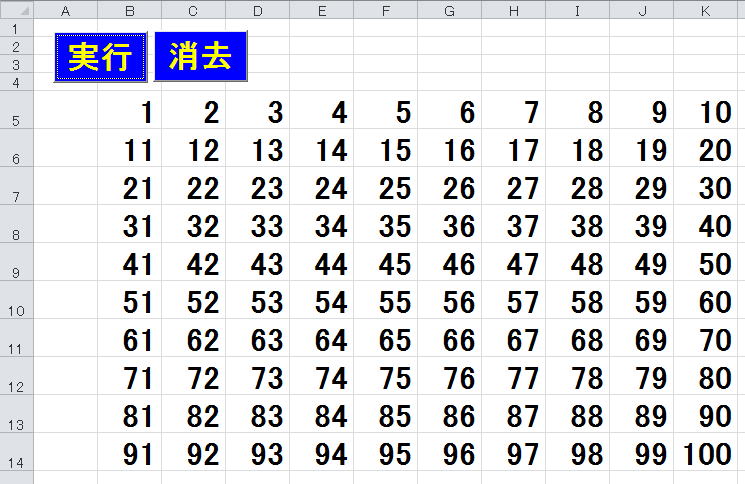
(ただし、3桁が表示できるようにシートのフォントサイズは変更してあります。
皆さんも試行錯誤で、適切なフォントサイズを探してください。)
