第12講 プロシージャの再帰的使用によって魔方陣を自動生成する
第２話 ２次元配列による方陣順列生成プログラム

コード例
Private Sub CommandButton1_Click()
　　Dim n As Byte, cn As Integer, x(10, 10) As Byte
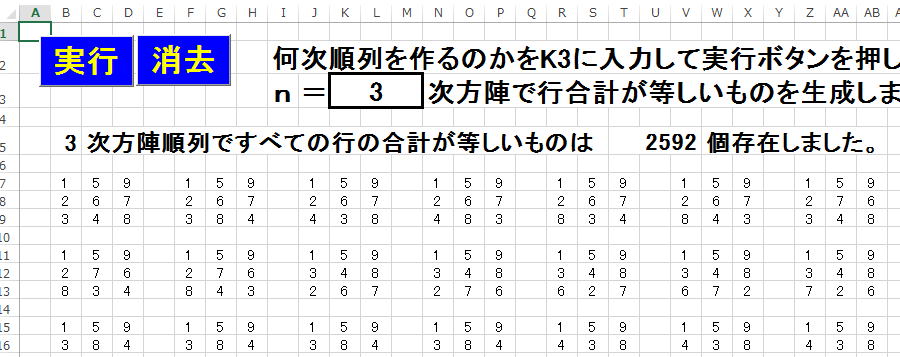
　　n = Cells(3, 11)
　　cn = 0
　　Call f(0, cn, n, x())
End Sub
Sub f(g As Byte, cn As Integer, n As Byte, x() As Byte)
　　Dim h As Byte, i As Byte, j As Byte, k As Byte, a As Byte, s As Integer, gi As Byte, gj As Byte
　　Dim ji As Byte, jj As Byte
　　a = cn Mod 10
　　s = Int(cn / 10)
　　gi = Int(g / n)
　　gj = g Mod n
　　For i = 1 To n * n
　　　　x(gi, gj) = i
　　　　h = 1
　　　　If g > 0 Then
　　　　　　For j = 0 To g - 1
　　　　　　　　ji = Int(j / n)
　　　　　　　　jj = j Mod n
　　　　　　　　If x(ji, jj) = x(gi, gj) Then
　　　　　　　　　　h = 0
　　　　　　　　　　Exit For
　　　　　　　　End If
　　　　　　Next
　　　　End If
　　　　If h = 1 Then
　　　　　　If g + 1 < n * n Then
　　　　　　　　Call f(g + 1, cn, n, x())
　　　　　　Else
　　　　　　　　For j = 0 To n - 1
　　　　　　　　　　For k = 0 To n - 1
　　　　　　　　　　　　Cells(5 + j + (n + 1) * s, 2 + k + (n + 1) * a) = x(j, k)
　　　　　　　　　　Next
　　　　　　　　Next
　　　　　　　　cn = cn + 1
　　　　　　End If
　　　　End If
　　Next
End Sub
参考ファイル

解説
頭が混乱するでしょう。
　　gi = Int(g / n)
　　gj = g Mod n
と
　　　　　　　　ji = Int(j / n)
　　　　　　　　jj = j Mod n
がミソです。
１次元gを２次元（ｉ，ｊ）に対応させるには
　　gi = Int(g / n)
　　gj = g Mod n
とすれば良いですし、
１次元jを２次元（ｉ，ｊ）に対応させるには
　　　　　　　　ji = Int(j / n)
　　　　　　　　jj = j Mod n
とすれば良いのです。

では、皆さんこれを改良して魔方陣自動生成プログラムへと
歩を進めることにしましょう。
ただし、２次魔方陣は存在しませんし、
１次魔方陣は面白くも何ともありませんから、
ｎは３以上の条件が加わります。

ｎ次魔方陣のすべての行・列・対角線の合計はｎ×（ｎ×ｎ＋１）／２
なぜならすべての総和が
１＋２＋３＋・・・＋ｎ×ｎ＝ｎ×ｎ×（ｎ×ｎ＋１）／２
です。これは等差数列の和の公式です。
初項と末項を足して、それに項数を掛けて２で割れば良い訳です。
そして、総和をｎ（＝行数＝列数））で割ったｎ×（ｎ×ｎ＋１）／２が
魔方陣のすべての行・列・対角線の合計という訳です。

まずすべての行（横）の合計がｎ×（ｎ×ｎ＋１）／２になっているときだけ、
エクセルにはき出させるように変更を加えましょう。

第１話へ　第３話へ

初心者のためのc++ vc++ c言語 入門 基礎から応用までへ
初心者のための excel 2007 2010 2013 vba マクロ 入門 基礎から応用まで
初心者のための世界で一番わかりやすいVisual C++入門基礎講座
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座へ
vb講義トップへ
ＶＢ講義基礎へ
専門用語なしのC++入門へ
専門用語なしのJava入門へ
専門用語なしのVBA入門

数独のページ
魔方陣のページ
数学研究室に戻る
本サイトトップへ