第7話 グローバル変数を利用しない普遍的な順列生成プログラム例
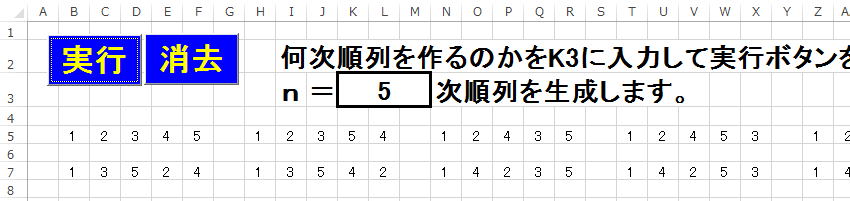
コード例
第11講 プロシージャの再帰的使用によって順列を生成する
第7話 グローバル変数を利用しない普遍的な順列生成プログラム例

コード例
Private Sub CommandButton1_Click()
Dim n As Byte, cn As Integer, x(15) As Byte
n = Cells(3, 11)
cn = 0
Call f(0, cn, n, x())
End Sub
Sub f(g As Byte, cn As Integer, n As Byte, x() As Byte)
Dim h As Byte, i As Byte, j As Byte, a As Byte, s As Long
a = cn Mod 10
s = Int(cn / 10)
For i = 1 To n
x(g) = i
h = 1
If g > 0 Then
For j = 0 To g - 1
If x(j) = x(g) Then
h = 0
Exit For
End If
Next
End If
If h = 1 Then
If g + 1 < n Then
Call f(g + 1, cn, n, x())
Else
For j = 0 To n - 1
Cells(5 + 2 * s, 2 + (n + 1) * a + j) = x(j)
Next
cn = cn + 1
End If
End If
Next
End Sub
解説
渡す側の引数名と渡される側の引数名は
同一にする必要はありませんが、
わかりやすさを優先して今回は同じにしてあります。
今回作った順列を方陣状に並べて、
すべての行・列・対角線の合計が同じになるものだけを、
エクセルのシートにはき出せば、
魔方陣の自動生成プログラムが完成できます。
次講では、プロシージャの再帰的使用によって
魔方陣の自動生成に挑戦します。
ただし、この単純な方法では理論的には100次魔方陣でもできますが、
実際のところは4次までが限界です。
4次魔方陣は、対称なものなども別に数えると、
7040個ありますが、すべてはき出すには1時間程度要します。
5次魔方陣では、約20億個存在しますし、
この方法では1個を作り出すのに、
10分ぐらいかかりますから、
20億個全部作り出す頃には、
自分の命はとっくに終わっていることでしょう。
私が組んだ最速の魔方陣自動生成プログラムだと、
26次魔方陣でも1秒に数百個生産のレベルですが、
これに至るには様々な工夫が必要です。
この入門講義に最後までついて来て頂ければ、
あなたも1秒で26次魔方陣などを1秒で数百のレベル
で作り出させることが可能になります。
どうか末永くおつきあいください。
さて、次講の第1話の課題を出して、
第11講を閉めることにしましょう。
課題は今回のファイルを改良して、
順列を方陣上に並べることです。
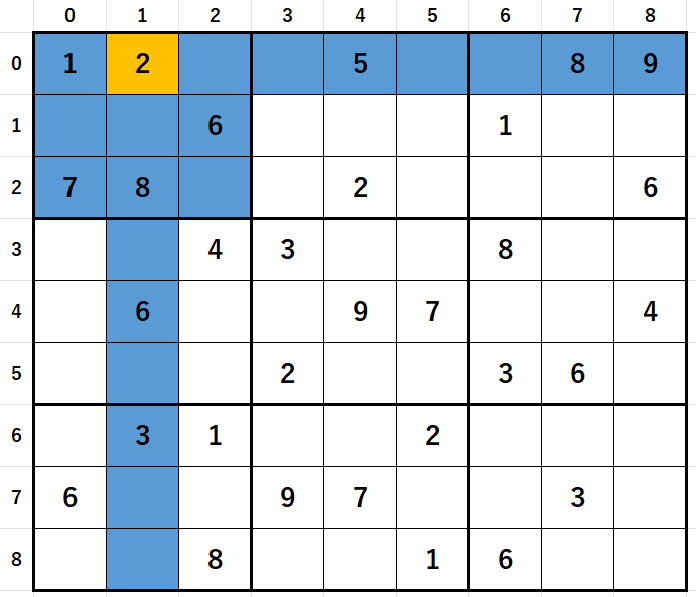
ただし、3次方陣順列が限界です。
3次方陣順列は3×3=9次順列で、
4次方陣順列なら4×4=16次順列になってしまうからです。
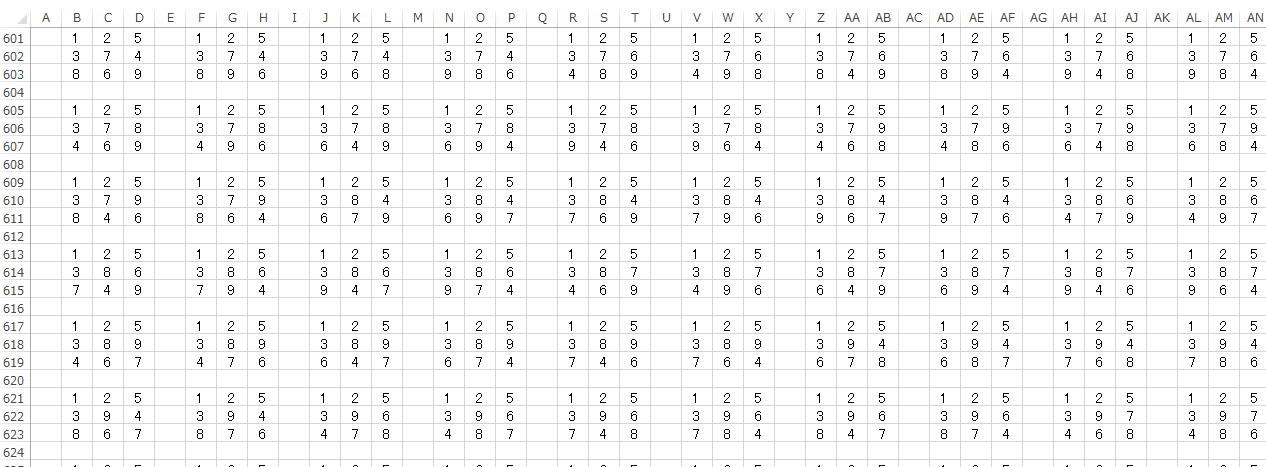
3次魔方陣の段階で延々と続きます。
9!=1×2×3×・・・×9=362880個生産されます。
初心者のためのc++ vc++ c言語 入門 基礎から応用までへ
初心者のための excel 2007 2010 2013 vba マクロ 入門 基礎から応用まで
初心者のための世界で一番わかりやすいVisual C++入門基礎講座
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座へ
vb講義トップへ
VB講義基礎へ
専門用語なしのC++入門へ
専門用語なしのJava入門へ
専門用語なしのVBA入門
数独のページ
魔方陣のページ
数学研究室に戻る
本サイトトップへ