第1話 順列のすべてを生成させる普遍的なプログラムを組むことの難しさについて
第10講でも申し上げましたように、
実は普遍的な(一般的な)順列生成プログラムを組むことは
(普遍的な順列生成プログラムの普遍的という意味は、
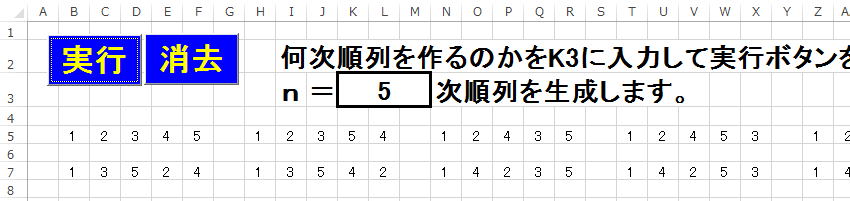
123・・・nのn個なる順列をn次順列と名付けるなら、
nがなんであっても生成できるという意味です。
 )、
)、大変難しい課題です。
もしこれが簡単なら、
生成した順列を正方形状に並べて
第11講 プロシージャの再帰的使用によって順列を生成する
第1話 順列のすべてを生成させる普遍的なプログラムを組むことの難しさについて
第10講でも申し上げましたように、
実は普遍的な(一般的な)順列生成プログラムを組むことは
(普遍的な順列生成プログラムの普遍的という意味は、
123・・・nのn個なる順列をn次順列と名付けるなら、
nがなんであっても生成できるという意味です。
 )、
)、
大変難しい課題です。
もしこれが簡単なら、
生成した順列を正方形状に並べて
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 9 | 8 |
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 8 | 7 | 9 |
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 8 | 9 | 7 |
・・・
(9次順列で例示)
その中で
すべての縦の合計
すべての横の合計
2つの対角線の合計
が同じになっているものを探し出せば、
| 8 | 1 | 6 |
| 3 | 5 | 7 |
| 4 | 9 | 2 |
魔方陣は完成するのです。
魔方陣といえど順列の1つを
正方形状に並べたものにすぎないのです。
ですから、すべての順列を作り出すプログラムが完成すれば、
魔方陣自動生成プログラムまで後1歩にすぎないのです。
普遍的な(一般的な)順列生成プログラムを組めという課題を
初心者が与えられたなら、
途方に暮れるだけでしょう。
もちろん、意欲のある方は次話を読まないで
挑戦されても結構ですが、
100人挑戦されても、100人とも何をしたら良いか、
見当も付かず、手も足も出ない状態になるのではないでしょうか。
(もし、ノーヒントで組める方がいらっしゃるなら、
あなたは天才です。
組めた方は、是非とも魔方陣自動生成プログラムに挑んでみてください。
ただし、ここで述べた方法では5次魔方陣までが限界ですし、
5次魔方陣でもすべての魔方陣を生成するには、
スーパコンピュータでも1000年以上かかるでしょう。
4次魔方陣は、鏡像や線対称なものなども別に数えるなら、
すべてで7040個ありますが、
この方法ではすべて生成するのに、
パソコンでは20分以上かかります。)
というわけで、課題とせず次話において解答例を示します。
かなり難解なプログラムですので、第3話以降では
5,6話を投入して解説していきます。
初心者のためのc++ vc++ c言語 入門 基礎から応用までへ
初心者のための excel 2007 2010 2013 vba マクロ 入門 基礎から応用まで
初心者のための世界で一番わかりやすいVisual C++入門基礎講座
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座へ
vb講義トップへ
VB講義基礎へ
専門用語なしのC++入門へ
専門用語なしのJava入門へ
専門用語なしのVBA入門
数独のページ
魔方陣のページ
数学研究室に戻る
本サイトトップへ