| 第1講 |
魔方陣って何? |
| |
数独って何?Javaって何?
Eclipseって何? |
第5話 小さな目的の追求が大きな成果・新しい領域を生む
でも、なぜ魔方陣と数独からプログラミングを学ぶなの?
の疑問はまだ残っているのではないでしょうか。
皆さんご存じですか。
数学の世界では、小さな目的を追求していたら、
気がついたら広大な新しい研究領域や研究部門を築いていた、
ということはしばしば起きていることなのです。
有名なのはフェルマー予想です。
1990年代に証明されてフェルマーの定理になっていますが、
人類はこの定理を証明するまで400年ぐらいを要したのです。
なぜなら、フェルマーが予想した年代は16世紀であったからです。
フェルマーの定理とは次のような単純な定理です。
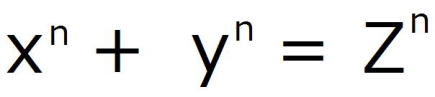
を満たす整数解は、n≧3では存在しないというものです。
この定理自体はおそらく重要性はないでしょう。
証明できてもできなくても、
数学者以外にとってはどうでも良いことであったでしょう。
しかし、数学者たちはこの予想の証明にこだわりました。
そして、予想を証明しようとして数学者たちはさまざまなツールや
数学の新しい領域を開拓していったのです。
定理自体の証明に意義があったのではなく、
証明しようと努力を重ねていく内に、
数学の研究領域が広がり、さまざまな研究部門が生まれていった、
この点にフェルマーの定理の本当のすばらしさがあります。
もうひとつ例を挙げるとすれば、
ユークリッドの第5公準でしょう。
第5公準とは、
直線外の1点を通る平行な直線は1本しか引けないというものです。
ユークリッドは証明を必要としない公理(公準)の一つと考えたわけですが、
ユークリッド以降の数学者たちは、
他の4つの公理(公準)に比べると、
複雑なので実は4つの公理から証明できる定理なのではないかと考え、
証明を試みるのです。
こちらは、2000年以上の奮闘の歴史があります。
いろいろな巨人(例えば、ニュートン)達が証明に挑みましたが、
2000年に渡り数学者達の挑戦を跳ね返してきたのです。
ですが、ユークリッドの第5公準を証明しようとしてきた努力が、
非ユークリッド幾何学の発見、
そしてアインシュタインが非ユークリッド幾何学を物理学に適用して、
相対性理論を作り出すという、
予想だにしない成果を引き出したのです。
非ユークリッド幾何学・相対性理論・ダーウィンの進化論は、
科学の3大発見といわれています。
第5公準を証明しようとする営みが、
科学の3大発見の内の2つを導き出してしまったのです。
以上の二つの出来事に比べれば、余りに小さなことですが、
私にも同様な体験があります。
私が塾教師をしているとき、
中学生から5次魔方陣の作り方を教わりました。
その方法とは、
1行目真ん中にに1を入れる。
| 17 |
24 |
1 |
8 |
15 |
| 23 |
5 |
7 |
14 |
16 |
| 4 |
6 |
13 |
20 |
22 |
| 10 |
12 |
19 |
21 |
3 |
| 11 |
18 |
25 |
2 |
9 |
そして、斜め上に上がりながら順に2,3,4,・・・と入れて行く。
ただし、上がない場合には一番下に、右がない場合は一番左に行く。
| 17 |
24 |
1 |
8 |
15 |
| 23 |
5 |
7 |
14 |
16 |
| 4 |
6 |
13 |
20 |
22 |
| 10 |
12 |
19 |
21 |
3 |
| 11 |
18 |
25 |
2 |
9 |
斜め右上にすでに数字が入っている場合(上の図の場合は1)は、
その列(上の図の場合は5の列)の1つ下に入れる。
| 17 |
24 |
1 |
8 |
15 |
| 23 |
5 |
7 |
14 |
16 |
| 4 |
6 |
13 |
20 |
22 |
| 10 |
12 |
19 |
21 |
3 |
| 11 |
18 |
25 |
2 |
9 |
以下同様に入れていって、
| 17 |
24 |
1 |
8 |
15 |
| 23 |
5 |
7 |
14 |
16 |
| 4 |
6 |
13 |
20 |
22 |
| 10 |
12 |
19 |
21 |
3 |
| 11 |
18 |
25 |
2 |
9 |
というものでした。
私は、どうしてこんな単純なやり方で5次魔方陣ができてしまうか、
不思議でならず、魔方陣の研究を始めたわけです。
(その研究の結果が魔方陣のページというわけです。)
そして、パソコンと出会ったとき、
魔方陣をコンピュータに考えさせ、
コンピュータ自らに発見させるという、
という考えに囚われるようになったのです。
より高速な処理を求めていく内に、
BASIC、C言語、パスカル、C++、Java
などの言語を習得し、
今ではvc++の入門系ではGoogleでダントツのトップである
初心者のためのc++ vc++ c言語 入門 基礎から応用まで
VBA入門系では、『VBA 2010』などでトップになる
初心者のための excel 2007 2010 2013 vba マクロ 入門 基礎から応用まで
の著者になっていたのです。
魔方陣という人から見ればどうでも良いものにこだわっていたら、
知らない内にいろいろなプログラミング言語を身につけていたのです。
小さな目的の追求が大きな成果・新しい領域を生む
という表題の意味がお分かりでしょうか。
第4話へ 第6話へ

初心者のためのc++ vc++ c言語 入門 基礎から応用までへ
初心者のための excel 2007 2010 2013 vba 入門 基礎から応用まで
初心者のための世界で一番わかりやすいVisual C++入門基礎講座
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座へ
vb講義トップへ
VB講義基礎へ
専門用語なしのC++入門へ
専門用語なしのJava入門へ
専門用語なしのVBA入門
数独のページ
魔方陣のページ
数学研究室に戻る
本サイトトップへ