private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
int i;
int j;
String^ w="";
for(i=0;i<10;i++){
a[i]=i;
}
for(i=0;i<10;i++){
w=w+L" "+a[i].ToString();
}
label1->Text=w;
w=L"";
for(i=0;i<4;i++){
for(j=0;j<4;j++){
b[i][j]=rand() % 16;
}
}
for(i=0;i<4;i++){
w1[i]=0;
w2[i]=0;
for(j=0;j<4;j++){
w1[i]=w1[i]+b[i][j];
w2[i]=w2[i]+b[j][i];
}
}
for(i=0;i<4;i++){
for(j=0;j<4;j++){
if(b[i][j]<10){
w=w+L"0"+b[i][j].ToString()+L" ";
}
else{
w=w+b[i][j].ToString()+L" ";
}
}
if(w1[i]>=10)w=w+L" "+w1[i];
if(w1[i]<10)w=w+L" "+L"0"+w1[i];
w=w+L"\n";
}
w=w+L"\n";
for(i=0;i<4;i++){
if(w2[i]<10){
w=w+L"0"+w2[i].ToString()+L" ";
}
else{
w=w+w2[i].ToString()+L" ";
}
}
label2->Text=w;
・
・
・
w1[0]は1行目の合計
w1[1]は2行目の合計
w1[2]は3行目の合計
w1[3]は4行目の合計
のための変数です。そして、
w2[0]は1列目の合計
w2[1]は2列目の合計
w2[2]は3列目の合計
w2[3]は4列目の合計
のための変数です。
では、
for(i=0;i<4;i++){
w1[i]=0;
w2[i]=0;
for(j=0;j<4;j++){
w1[i]=w1[i]+b[i][j];
w2[i]=w2[i]+b[j][i];
}
}
の部分の動きを
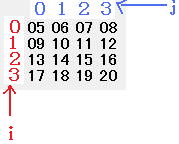を例にトレースしてみましょう。Ⅰ i=0の場合
w1[i]=0;
w2[i]=0;
によってw1[0]=0，w2[0]=0
となります。
ⅰ j=0のとき
w1[0]←w1[0]+b[0][0]
w2[0]←w2[0]+b[0][0]
によって、w1[0]=b[0][0]すなわちw1[0]=5
w2[0]=b[0][0]すなわちw2[0]=5
ⅱ j=1のとき
w1[0]←w1[0]+b[0][1]
w2[0]←w2[0]+b[1][0]
によって、w1[0]=5+6すなわちw1[0]=11
w2[0]=5+9すなわちw2[0]=14
ⅲ j=2のとき
w1[0]←w1[0]+b[0][2]
w2[0]←w2[0]+b[2][0]
によって、w1[0]=11+7すなわちw1[0]=18
w2[0]=14+13すなわちw2[0]=27
ⅳ j=3のとき
w1[0]←w1[0]+b[0][3]
w2[0]←w2[0]+b[3][0]
によって、w1[0]=18+8すなわちw1[0]=26
w2[0]=27+17すなわちw2[0]=44
以上によって、1行目と1列目の合計が計算されました。
Ⅱ i=1の場合
w1[i]=0;
w2[i]=0;
によってw1[1]=0，w2[1]=0
となります。
ⅰ j=0のとき
w1[1]←w1[1]+b[1][0]
w2[1]←w2[1]+b[0][1]
によって、w1[1]=b[1][0]すなわちw1[0]=9
w2[1]=b[0][1]すなわちw2[0]=6
ⅱ j=1のとき
w1[1]←w1[1]+b[1][1]
w2[1]←w2[1]+b[1][1]
によって、w1[1]=9+10すなわちw1[0]=19
w2[1]=6+10すなわちw2[0]=16
ⅲ j=2のとき
w1[1]←w1[1]+b[1][2]
w2[1]←w2[1]+b[2][1]
によって、w1[1]=19+11すなわちw1[1]=30
w2[1]=16+14すなわちw2[0]=30
ⅳ j=3のとき
w1[1]←w1[1]+b[1][3]
w2[1]←w2[１]+b[3][1]
によって、w1[1]=30+12すなわちw1[1]=42
w2[1]=30+18すなわちw2[１]=48
以上によって、2行目と２列目の合計が計算されました。
Ⅲ i=2 Ⅳ i=3 の場合については皆さんがトレースしてみてください。
では、また課題を出して今回の話題を閉じます。
対角線の合計を求めましょう。また、
についても列・行・対角線合計を求めましょう。
