Private Sub CommandButton1_Click()
Dim a(2, 3, 4, 5) As Integer
Dim b(11, 29) As Integer
Dim i As Integer, j As Integer, k As Integer, l As Integer
For i = 0 To 11
For j = 0 To 29
b(i, j) = 30 * i + j + 1
Next
Next
Dim ii As Integer, kk As Integer
For i = 0 To 11
ii = Int(i / 4)
j = i Mod 4
For k = 0 To 29
kk = Int(k / 6)
l = k Mod 6
Cells(5 + 6 * ii + kk, 1 + 7 * j + l) = b(i, k)
Next
Next
For i = 0 To 11
ii = Int(i / 4)
j = i Mod 4
For k = 0 To 29
kk = Int(k / 6)
l = k Mod 6
a(ii, j, kk, l) = b(i, k)
Next
Next
For i = 0 To 2
For j = 0 To 3
For k = 0 To 4
For l = 0 To 5
Cells(24 + 6 * i + k, 1 + 7 * j + l) = a(i, j, k, l)
Next
Next
Next
Next
End Sub
実行シート
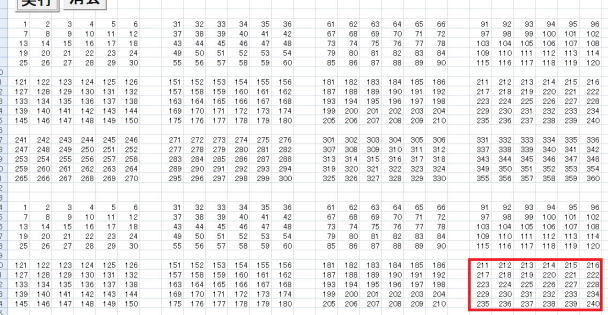
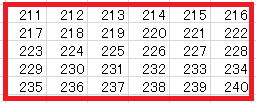
どうです。結構難しいですよね。頭の体操になります。
でも、2次元を1次元で表現できることに気がついたとき、
私の魔方陣プログラムの研究は跳躍することになるのです。
『魔方陣の生成は、結局は順列の作成と本質的に同じだ!』
私の魔方陣研究にとってひとつの画期をなす大事件だったのです。
この発見がなければ、数々の魔方陣作成プログラムや数独問題自動生成ソフトは決して生まれなかったのです。
2次元を1次元に翻訳する、あるいは、1次元を2次元に翻訳するという考え方を利用して、
いよいよ魔方陣の自動生成に挑戦します。
前に作った4次魔方陣と6次魔方陣は規則性を適応しただけのものですが、
今回作るものは、コンピュータが自分で考え解答のすべてを発見してしまうものです。
3次なら8個ですし、4次なら7040個です。
(ただし、鏡像や対象変換像なども含んでいます。
それらを同じものと見なすと、3次魔方陣は1個、4次魔方陣は880個の解答をもっています。)
そして、やがては数独問題の自動作成にも挑戦します。
尚、今回作る自動生成プログラムは、本当に原始的なもので最速のものに比べれば20次魔方陣あたりでは、
作成速度は1兆分の1ぐらいです。
理論的には、何次魔方陣でも作成可能ですが、現実には4次魔方陣あたりが限界です。
4次魔方陣でさえすべてを作り出すには10分程度かかってしまいます。
5次魔方陣では、100個に限定したとしても2時間ぐらいかかってしまうでしょう。
26次魔方陣などを1秒に数百個というレベルで作れるようにするには
(魔方陣(細胞構成法)を参照してください)、かなりの改善が必要です。
今回は、本当に長く険しい旅の始まりの一歩にすぎないのです。
第7話へ 第15講第1話へ
