弾力的学力観Ｐ２

　　したがって、確かに数学嫌いができあがる必然性があるのであるが、彼らの学力について誤解してはならない。それは、彼らが一度も算数や数学の基礎を理解したことがないのではないということである。基礎を理解したことがないために現在の状態があるわけではないということである。２章でもいったように、小学校や中学校の先生たちがいろいろな諸制約があったにしろ、決して学力不振の生徒たちを、何もせず放置していたのではない。可能な範囲で、小中学校の先生たちは、補習などをし、あるいは個別指導などをし、ふつうの生徒以上に面倒をみてきたのである。そういう先生たちの努力によって、学力不振の生徒たちも一度は理解した体験を多く持っているのである。

　それでは、彼らにおいては何が問題なのであろうか。私もＸＸ高校に赴任してからおよそ６年間に渡り特別指導の名の下に、学力不振の生徒たちをマンツーマンに近い形で指導してきた。特別指導は普段の授業ではわからない、いろいろな生徒の側面を知ることができる。私は新しくＸＸ高校に赴任してきた先生方には、必ずこの個別指導を勧めている。生徒の実態を把握するのに最も優れた方法の一つである。学力不振の生徒の学力の構造を把握することができる。どんな点で生徒たちが誤解をし、どんな点がわかりにくいのかを把握できるのである。後で詳しく評論するが、どんな点がわかりにくいのかという問題は、指導者がどんなに教科書や参考書などで教材を研究してもわからない。指導者にとってわかりやすいということと生徒にとってわかりやすいということは天と地ほど違うからなのである。この論考においてすでに指摘したし、これからも再三に渡って指摘することであるが、生徒の住んでいる世界と指導者が住んでいる世界は次元の違う世界なのである。私はそれぞれが住んでいる世界、あるいは発想の基盤・座標、認識の枠組・エピスティーメをパラダイムと呼ぶ。この用語を使うならば、生徒のパラダイムは指導者のパラダイムとは違う。それはユークリッド幾何学と非ユークリッド幾何学のパラダイムが違うように違うのである。この点はいくら強調しても強調しすぎということはない。指導者は常に独善に陥ってはいけない。生徒から学ばなければならないのである。生徒は、先生の最大の先生である。

　さて、生徒の学力というより能力の問題点はいったい何であろうか。最大の問題点は、彼らの学力が持続しないということなのである。正負の計算など、指導すれば彼らに理解させることはできる。しかしながら、すぐに忘れてしまうのである。彼らの記憶力は、１日いや場合によっては数十分しか持続しない。理解できたとしても、２０～３０分も自転車を漕いで家に帰るまでに彼らの脳髄から消えてしまうのである。指導をうまずたゆまず何度も繰り返したとしてもである。

　もう一つの問題点は、スイッチの切り替えができないということである。公式の使い方を指導した後で、この公式を直接使う問題を与えると生徒は解くことができる。しかしながら、いろいろな公式を使う問題がアトランダムに並んでいるととたんにできなくなってしまう。例えば、第１章で出した例であるが、５－３＋２を０と答えた生徒がいる。この生徒が決して小学校１年生程度の学力しかないわけではない。正負の計算を指導した後だったので、誤ってしまったのである。この問題は中学１年で学ぶ正負の計算ではなく、小学１年生でもできる問題であるというようにスイッチの切り替えができないのである。逆の側面もある。数学と物理で全く同じ問題、例えば三角比の問題や速さの問題が出てきたとき、彼らは別の問題であると思ってしまう。彼らにはチャンネルは一つしかない。狭視野が彼らの特徴である。柔軟に考えられないのである。

　第４の問題点は、抽象的思考を徹底的に苦手としているということである。５＞３は理解できても、Ｘ＞３は理解できないのである。ここでのＸは、４でもあるし５でもあるしその他でもあるし、逆に４でも５でもその他でもない一般的なもの・抽象的なものである。文字が入ると巨大なる拒否反応を示すのである。α、βなどの新しい文字が出てくるだけでそこになにか深遠な意味があるのではないかと思ってしまう。Ｘ＞３をさらに数直線に書くとなると混乱の度合いは、極限に達する。この点に関連して第５の問題点が出てくる。

　それは、彼らの思考は常に意味やイメージを伴っていないということである。これは彼らの思考が左脳だけに偏っているということである。極端に手順化しているものしか、彼らの頭脳は受け付けない。その思考には常に意味が伴っていない。彼らに概念を理解させることは非常に困難なのである。意味のない計算以上のことをさせるには、相当の工夫を必要とする。彼らが右脳を使わないのは、彼らの能力だけの問題ではない。現代の算数及び数学教育の問題である。残念ながら、現在の教育は左脳中心の指導である。生徒が理解できないとき、安易な指導は手順化でありアルゴリズム化である。われわれは、アルゴリズム化に頼りすぎているのである。この現代算数・数学教育の問題点、すなわち左脳に偏った教育になっているという問題点に関しては、後に独立の論文を書く予定である。また、第５章の小ステップ教育でももう一度触れられるだろう。とにかく、われわれが右脳を使う指導をしていたならば、ノーベル賞の受賞者はもっと多かったはずである。細かく論じれば、まだまだ彼らの問題点はある。しかし、後論のために必要な論点はすでにそろった。その中でも特に必要な論点は、第１と第２で指摘した点、すなわち忘却と狭視野（スイッチの切り替えができない）である。その点を確認して、この論考において最も大事な核心をなす次の考察に移ることにしよう。

　かつて教育困難校の先生方が、生徒たちは基礎学力がない、したがって小中の基礎に戻り遅れを取り戻さなければならないと考え、高校生に小学校や中学校の教科書を与えたことがあった。その情熱は是非とも認めなければならないが、根本的に誤った考えである。高校生のプライドという問題を差し引いたとしてもである。基礎に戻らなければならない、という考えの基底にあるものは次のような学力観である。数学は積み重ねの学問である。そして基礎から出発し、学年の進行とともに次第に複雑になり高度になっていく。したがって、小学校よりも中学校の数学の方が難しく、さらに、中一よりは中二の方が難しい。一般的に、基礎がなければ次の学習は不可能ではないにしろ困難である、と考えられているのである。こうした学力観の中で、Ａ君は中学２年程度の学力だとか、Ｂ君は小学校中学年程度の学力しかないなどと評価されるのである。私はこれを固定的学力観と呼んでおきたい。

　この固定的学力観には二つの認識の誤りがある。一つは、学力不振生徒たちは理解力がないために、基礎ができないと考えている点である。これは全く誤った考えである。第３章で述べたように、学力不振生徒たちの能力の問題点は、理解力というより記憶力の方にあるのである。すでに述べたように小中学校の先生方は、落ちこぼれをつくるまいと熱心である。学力不振生徒児童などに補習などをし、一度は彼らに理解させたことが多いのである。高校に入学してくる学力不振生徒たちは、先生たちが放置していたためにそうなったのではなく、９年間に渡り先生方が可能な範囲で努力した結果生まれたのである。うまずたゆまない努力の結果生まれたのである。それをたった数年間で取り戻そうというのが、小中の教科書を与えようという考えなのである。

　第二の誤りの点に話を移そう。一般的には、学年が進行すればするほど難しくなると考えられている。例えば、微分は小４、５で学ぶ分数の計算より難しい、というわけだ。これはある意味では正しい。ある意味ではというのは、指導者のパラダイムにおいてはということである。指導者の座標・地平においては、微分が高等数学であることは疑いのない真理である。

　だが、コペルニクス的転回をして座標を生徒のパラダイムに移すならば、様相は一変してしまう。生徒にとっては微分の初歩の計算ならば、分数の足し算・引き算の方が難しいのである。たとえば、の微分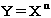を考えてみたまえ。この計算のアルゴリズムは、分数の足し算よりはるかに簡単である。実はこっちこそが真理なのである。この簡単な真理をわれわれは見落としているのである。よく考えてみると、このような事例はたくさんある。本来から言えば、というより指導者の立場から言えば、次の二次方程式は前者のほうがはるかに簡単である。　

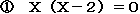
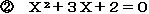
ところが、生徒にとって簡単なのは後者のほうである。指導者にとって簡単ということと生徒にとって簡単ということは、天と地ほどの差があるのである。

　だから、この観点に立ったとき学年が上に行けばいくほど難しくなるとはいえないのである。したがって、あの子の学力は中一程度だという評価は間違っているである。正しくは、中一の方程式ができなくても、中三の因数分解ができたりするのである。学力は弾力的に評価しなければならないのである。私は新しい学力観として弾力的学力観を提唱したいのである。断って置くがこれは文部省のいう「新しい学力観」とは何の関係もない。「新しい学力観」は、誤った古典的な学力観である固定的学力観を前提にしている。したがって、「新しい学力観」は古典的学力観に属するのである。　　　　　　　　　　　　　　　

　私は、序章において生徒の意欲を問題にしない教師には辞表を提出してもらった方が良いと書いたが、それは実は極端な言い方であり、私の本心ではない。なぜなら人は変わりうるからである。私は、教員の評価についても弾力的に評価するべきであると考えている。職場における教員評価はあまりにも短絡的であるように思われるからである。例えば、ある人が２年くらい指導がうまく行かなかったり授業がうまくいかなかったりしたときに、決してダメ教員の烙印を押すべきではない。３年目ぐらいに花開く人がいるからである。むしろ新米の先生は、２～３年は修羅場を経験すべきである。どんなに熱心に生徒を指導しても、生徒が全くいうことを聞かなかった体験を持つことはその人の教師生活にとって、プラスになることだからである。ある意味では最初からうまくいってしまう人のほうが恐いのである。修羅場を経験した人は、簡単なことでは挫折しないであろう。順風満帆いった人は逆にちょっとしたことで、折れてしまう可能性があるだろう。また、人間の深みという点でも問題があるだろう。人は成長しうる。このあたりまえの考えが、不思議なほどに教育界には欠落しているように思うのである。人を育てるということは組織を強くしていくうえで重要な視点である。成功し伸びゆく企業は、この観点を強く持っている。ところが、最も教育的でなければならない教育の現場で、この視点が欠落している、あるいは弱いというのは皮肉である。もちろん生徒を評価するときにも同じく、弾力的に評価しなければならない。いままでダメ生徒であったらといっても、これからもダメ生徒と決めつけてはいけない。生徒こそ日々成長しているのである。

　話が脱線したのでもとに戻そう。算数・数学は学年が進行すればするほど、難しくなるとは言えない、と言ったが、これは二つの側面から考えられている。一つは、パラダイムすなわち視点・座標の問題であり、他の一つは、事象的な問題である。パラダイムの問題とは、事象的にはＡの問題の方がＢの問題より難しいとしても、生徒は逆に感じていることがあるということである。指導者と生徒の見方はしばしば反対であり得るのである。だから、すでに述べたようにいくら教材研究を机上でしたとしても、良い授業はできないのである。机上の研究ではっきりさせられるのは、理由・帰結の関係や因果関係などの事象的な関係だけである。ところが生徒の感じ方は、しばしば事象的な関係とは無関係であり、場合によっては逆関係でさえある。したがって、良い授業をしようと思うならば、机上の世界から飛び出て生きた教材である生徒の海へと旅立たなければならないのである。生徒に学ぶ以外にないのである。生徒こそが先生の最大の先生である。他の一つすなわち事象的な問題とは、アルゴリズムの問題である。初歩の微分の計算のアルゴリズムと分数の足し算のアルゴリズムを比較するなら、文句無しに分数のアルゴリズムの方が複雑である。ところが、われわれは先入観にとらわれ、微分の計算の方が複雑であると思いこんでいるのである。これらの錯覚こそが、底辺校とか教育困難校といわわれる学校の生徒に、高校数学を教授することは不可能だという考えの基礎の一つなのである。

　結論を先回りしていうならば、パラダイム（生徒の意識・構え＝生徒の基本的な認識系）の問題から考えても事象の問題から考えても、高校数学の方が小中の算数や数学より難しいとは、一概には言えないのである。内容によっては高校数学の方が簡単な場合もあり得るのである。したがって、教授法を工夫するならば底辺校とか教育困難校とかいわれる学校の生徒たちにも、高校数学を教授すること可能なのである。高校数学を指導することは決して不可能ではない。可能であるし、指導すべきなのである。

　こう述べると私には、だが基礎の不足はどうするのかと、不満に思っている読者の顔が浮かぶ。たとえば、定積分の計算の際には確かに分数の足し算・引き算ができなければ、計算することはできない。だから、やはり基礎からは始めなければならないというわけだ。だが、ここで是非とも考えてほしい。この定積分の問題以外に分数の基礎がなければ、絶対に指導でないという単元・領域がどれだけあるだろうか。定積分の計算であってさえも、工夫をすれば分数が出てこないようにすることもできるし、他の単元ならばなおさらそうである。数値さえ工夫すれば、分数が出てこないようにすることは、さほど難しいことではない。分数を絶対に必要とする単元はよく考えてみれば、少ないのである。それでも定積分の計算など、分数を必要とする場面も確かにある。実は基礎への還帰は、必要な範囲で行えば良いのである。