Ⅱ 略
ＸＸ高校に赴任して最初の２年間は、この問題の指導には成功しなかった。かなり時間をかけても、この問題ができるようになる生徒はクラスに数名しかいなかったのである。原因は教科書の例題が、あまりにも飛躍が大きすぎるのである。この問題を分析してみると、式の変形だけに限定しても次のような８ないし９段階のステップがあることがわかる。
① ｙ＝ｘ２＋２ｘ の変形
② ｙ＝ｘ２＋２ｘ＋３ の変形
③ ｙ＝２ｘ２－４ｘ の変形
④ ｙ＝２ｘ２－４ｘ＋４ の変形
⑤ ｙ＝－ｘ２＋４ｘ の変形
⑥ ｙ＝－ｘ２－４ｘ＋３ の変形
⑦ ｙ＝－２ｘ２－８ｘ＋５ の変形
⑧ ｙ＝２ｘ２＋３ｘ＋２ の変形
⑨ ｙ＝－２ｘ２＋５ｘ－５ の変形
①の変形 ②の変形
ｙ＝ｘ２＋２ｘ ｙ＝ｘ２＋２ｘ＋３
＝ｘ２＋２ｘ＋１－１ ＝ｘ２＋２ｘ ＋３
＝（ｘ＋１）２－１ ＝ｘ２＋２ｘ＋１－１＋３
＝（ｘ＋１）２ －１＋３
＝（ｘ＋１）２＋２
③の変形
ｙ＝２ｘ２－４ｘ
＝２（ｘ２－２ｘ）
＝２（ｘ２－２ｘ＋１－１）
＝２｛（ｘ２－２ｘ＋１）－１｝
＝２｛（ｘ－１）２－１｝
＝２（ｘ－１）２－２
④の変形
ｙ＝２ｘ２－４ｘ＋４
＝２ｘ２－４ｘ ＋４
＝２（ｘ２－２ｘ） ＋４
＝２（ｘ２－２ｘ＋１－１） ＋４
＝２｛（ｘ２－２ｘ＋１）－１｝＋４
＝２｛（ｘ－１）２－１｝ ＋４
＝２（ｘ－１）２－２ ＋４
＝２（ｘ－１）２－２＋４
＝２（ｘ－１）２＋２
⑤⑥⑦⑧⑨略
①と②の関係をよくみてほしい。②の構成細胞として①があることがわかるであろう。③と①の関係も同様である。また、③は④の構成細胞である。どの段階においても前のステップが次のステップの基礎になっているのである。そして、①はすべてのステップの基礎になっている。どのステップにおいても、必ず①が現れるのである。実は、先の例題には①から⑧までのすべての段階が混入されているのである。いかに飛躍が大きいかわかるであろう。教科書ではこの例題の解説は１ページも与えられてない。ということは、この例題の指導に想定している時間は、多く見積もっても１．５時間程度であろう。教科書をつくった先生たちははたして底辺校といわれる高校を１度でも経験したことがあるだろうか。私には残念ながら否としか思えない。その証拠は指導書である。指導書を読んでも少しも参考にならない。どんな点が生徒にとって分かりにくいのか、まったくといっていいほど指摘されていない。
教科書の無能さの指摘はこんなところにしておこう。①から⑨までの時間配分は各ステップについて２／３時間である。つまり３ステップについて２時間である。しかも各時間の間に２０分程度の小テスト実施するので、①から⑨までの指導は全部で７～８時間かかることになる。進学校の先生にとって信じられない時間であろう。だが、これぐらいが妥当な時間なのである。
式の変形の指導が終わった段階で始めて先のⅠおよびⅡの指導にはいることができる。Ⅰの指導でも３～４時間の指導が必要である。しかも式の変形の前に徹底したグラフの指導がなされているのである。そして先の注意でも述べたように、グラフと式あるいは値と結びつくように指導しなければならない。
この小ステップ指導は大変大きな成功を収めた。このときの期末テストは、平均点が９３台であり、満点者が１５名ぐらいいたのである。誤解を避けるために言っておくならば、決して問題のレベルを落としたのではないということである。高校数学教科書レベルの問題である。小ステップ教育の成果なのである。おそらくこの小ステップ教育を受けていないＸＸ高校生ならば、平均点は６０を越えないであろう。実際の私が赴任した最初の２年間はそうだったのである。ＸＸ高校のおいては、２次関数の最大値最小値の問題は指導できないというのが常識だったのである。
最初の２年間は、何十回一般形から標準形への変形を説明しても生徒は理解できなかった。３年目からこの小ステップ教育を取り入れて、それから平均点が鰻登りに登り、現在の平均点に達したのである。そして、この論文の冒頭の前奏曲に書いた教室の状態が出現するようになったのである。誰も私語せず、誰もよそ見をせず、誰も居眠りをせず、例外なく全員が計算に没頭する。教室は水を打ったように静かであり、する音はシャープペンを忙しくカリカリと動かす音だけがするのである。結論を言ってしまえば、前奏曲の問の答えは魔法でも何でもないのである。生徒の実態にあった指導さえすれば、生徒は２次関数の最大値・最小値の問題であろうとできるようになるのである。生徒にあれだけ拒絶反応を引き起こした問題であってもである。
６章 結論その１
正しい指導さえすれば、生徒は高校数学であっても理解し自分のものにすることができる。そして、生徒は数学を好きになるのである。なぜ生徒は数学が嫌いになってしまったか。それは理解できなかったからである。成果がなかったからである。成果のない意欲など絶対にありえない。（「新しい学力観」が言う成果のない意欲など形容矛盾である。）逆に言うならば、成果があれば意欲が生じるのである。われわれの実践が証明するところによれば、理解できるようになりさえすれば生徒は数学が好きになるのである。先にも書いたように、入学当初のアンケートによれば、９割の生徒が数学は嫌いであると答えている。ところが、２次関数の指導が終えた段階で同じアンケートをとってみると、３８名中３４人が数学が好きであると答え、嫌いと答えた生徒はわずか４名である。嫌いと好きが逆転してしまうのである。
第１章の問いに答えておこう。底辺校と言われる学校の生徒は特別の動機付けをしなければ、数学を好きになることはないという考えは、誤りである。高校数学の内容を、教科書の章立ての通りに指導していけば、生徒は数学が好きにあるのである。実際にアンケートで嫌いと答えた４名の生徒も、中学時代よりはかなり好きになり、好きと言えるまであと一歩であると答えている。実は特別の動機付けなど必要としないのである。理解さえさせてやれば生徒は数学が好きになるのである。生徒の実態にあった適切な指導さえすれば、生徒は必ず数学が好きになるのである。粘り強い指導さえ繰り返せば、生徒は好きになるのである。一番最後の章で生徒の感想をいくつかお見せするが、その感想文を読むならば、私が言っていることが少しも誇張でないことがわかるであろう。生徒は本質的に数学が好きなのである。生徒は強い知的好奇心を持っているのである。
７章 諸論点
結論の途中であるが、いくつか語り落とした諸論点をここにいれておくことにしよう。一つは繰り返しということについてである。学力不振生徒の大きな特徴は忘却である。したがって、指導の際気をつけなければならないことは、常に基礎的なこと・大事なことは繰り返し繰り返し指導することが必要である、ということである。基礎への帰還は常に必要な範囲で繰り返し行わなければならないのである。たとえば、６章の標準形の変形のステップ③④の指導の際には次の分配法則の確認が必要である。
ａ（Ｘ＋Ｙ）＝ａＸ＋ａＹ ａＸ＋ａＹ＝ａ（Ｘ＋Ｙ）
分配法則など何回もやっているから確認など必要ないと考えてはならない。常に基礎への還帰が必要なのだ。理由は忘却ということだけではない。スイッチの切り替えという問題も絡んでいる。
なぜなら、彼らは標準形の変形で使う公式 は因数分解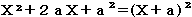
で使った完全平方の公式と同じであることに気がつかないのである。標準形への変形をさんざんやった後で、因数分解の問題 
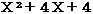を因数分解せよを出したとすれば、この問題に答えられないのである。彼らにはチャンネルは一つしかないのである。だから、常に基礎への還帰が行われなければならない。
われわれは繰り返しという事に次のような不安を抱く。生徒が飽きてしまうのではないかという不安である。だが無用の心配だ。生徒はそう感じていないからである。数学の指導者からすると、計算問題ばかりだと退屈してしまう。だから、生徒も退屈してしまうのではと心配するわけだ。だが、実践が証明するところによれば違う。生徒は同じような計算問題を不平も言わず、黙々とひたすらやり続ける。生徒は決して苦痛に思っていない。生徒はむしろ楽しんでいる。計算できることを喜んでいる。冒頭の前奏曲に書いた通り、生徒は因数定理による因数分解を３時間にわたり計算し続けたのである。計算が喜びなのだ。なぜか。理由は簡単である。それだけ彼らは数学に対する強いコンプレックスを抱いているのである。自分は数学なんてダメなんだと思いあきらめていた。自分の知性には、数学という高度なものは無縁であると思っていたのである。ところが高校にきて、中学時代よりはるかに複雑である数学を理解し、かつては自分とはまったく無縁であった高度な計算を自分でしていることは、驚異なのである。理解できるという事は喜びなのだ。高度な操作ができることは、無上の歓喜なのだ。人間がいかに知的好奇心をもっているかが、生徒たちの感想文からわかる。もしあなたが、ユーモアのセンスがないことで教師としての才能がないなどと思っているとすれば、無用な心配だ。生徒に理解させる力さえあれば、生徒は数学を好きになり、そしてあなたを好きになるであろう。理解ということはそれだけ大きいのである。生徒があなたに期待することは、数学を理解させてくれることなのだ。生徒は理解こそ最上の喜びなのだ。
脱線ついでに言うと、私はこの本論において特別の動機付けやユーモアなどは必要ないという事を強調している。これこそが本論の基本的なモチーフである。だが否定しているわけではない。特別の動機付けの研究やユーモアなどは、もちろんあった方が良い。私は、動機付けをまったくやっていないわけではない。むしろ可能な範囲で動機付けをしている。たとえば、魔方陣の話・対数の神秘・数学史・ゼノンのパラドックス・クレタ人の嘘など枚挙にいとまがない。だが、これらの努力は本質的でない。これらは小手先の技術である。普段の授業が大切なのだ。
逆説を言ってしまおう。特別な動機付けが必要なのはむしろ進学校のほうである。たとえば、数学が受験科目でない生徒に興味を持たせるのは大変なことである。中途半端に知的レベルが高いことが災いしている。底辺校の生徒に比べれば、素直さにかけるであろう。
数学を受験科目にしている生徒でさえ、本当の意味で数学に興味をもたせることは難しい。彼らは数学を手段としてしか見ていない。数学がいかにすばらしい学問であるか、わかってはいるまい。数学とは受験問題を解くことであると思っている。紀元前から研究され大事な学問であるとされてきた数学は、決して受験のための手段ではない。ヨーロッパでは哲学とともに学問の女王とされてきたのである。それを何の役にもたたないけれども、進学のためにやむを得ず勉強していると思っている生徒は、多数いるであろう。何と嘆かわしいことであろうか。
６章に関連づけてさらに一つの論点を付け加えておこう。６章で報告した期末テストの結果が与えた生徒への影響である。生徒がもっとも苦手としている単元は、１次関数や２次関数などの関数ある。そのコンプレックスの大きさたるや絶大なものがある。どうか１度で良いから生徒に聞いてほしい。いかに苦手であるかわかるであろう。ところがそのもっとも苦手とする単元で９０以上の点数が取れたのである。自分とは無縁だと思っていた関数を理解し、自分で最大値最小値を求めことができることは驚異なのである。自分があきらめていた可能性を知ることができたのである。これだけ自分を苦しめていた数学でもやればできるし、好きになり面白くなることを知ったのである。これは生徒にとっては革命的な事件と言って良い。高校時代で大きな思い出の一つになるであろう。その喜びたるや計り知れないものがある。生徒の書いた感想文を是非読んでほしいと思う。
テストの平均点についても一言述べておきたい。平均が９０を越えるテストは怠慢ではないかという批判もあると思う。指導が研究によってより高くなったとすれば、テストもそれに相応してレベルをあげるべきであるという考え方もあるであろう。それはまったくその通りである。だが、自信を根底から失っている生徒に１度は自信を回復させる必要があるのである。点数自身が生徒に与えた衝撃を是非知ってほしい。
再び結論に入る前に、もう一つだけ断っておきたい。それは、生徒の実態にあった授業をすれば、自然に生徒が授業を聞くようになると考えるならば、大きな間違いであるということである。すばらしい授業をすれば、自然に生徒は授業を聞くようになる、この考えは意外に広く流布されている考えである。だから、定時制の物理の先生たちが、強烈な動機付けによって生徒を引きつけようとした実践などが行われたのである。たとえば、剣山の上に裸で乗るなどの動機付けをした。だが、すばらしい授業をすれば、自然に生徒が授業を聞くようになると考えているならば、まさに幻想である。すばらしい授業をしなければ、自然に授業を聞かなくなるということは真実である。だが、すばらしい授業をすれば、自然に聞くようになるということは真実ではない。ＸＸ高校などの底辺校とか教育困難校とかいわれる高校に入学してくる生徒のほとんどの生徒が、数学に強い劣等感を抱き、数学にアレルギー反応を持っているのである。ほとんどの生徒が数学嫌いなのである。ほとんどの生徒が数学のすばらしさを理解していないのである。どんなにすばらしい授業をしようとも、残念ながら彼らは聞く耳を持っていないのである。聞くようにさせるために確かに先の物理の先生のように、強烈な動機付けをすることも一つの方法である。だが、すぐに種切れになってしまう。そして、生徒たちはより強烈な動機付けでなければ、聞かなくなってしまうのである。強烈な動機付けを試みる人は、生徒の知的好奇心を心からは信じていないのである。普通の教材でも、生徒は必ず興味を示すようになるとは信じていないのである。逆に言うならば、数学や物理を好きな自分たちを変わり者の人間であるとみなしているのである。ではどうすれば、生徒に聞く耳を持たせることができるだろうか。答えは簡単である。しつけをするということである。入り口を造らなければ、どんなにすばらしい授業をしようとも生徒は入ってくることはない。学力不振に陥った原因は、彼らの能力とともに、学習の姿勢も大きい。彼らに欠けているものは粘り強さである。頂上に登っていくためには、一歩一歩登って行くしかない。たとえ頂上が見えなかったとしてもである。頂上が見えないとき、確かに登ることがいやになってしまうことがある。だが、知的優秀児たちはこのとき非常に粘り強い。ある英才教室で、小学校低学年の子どもたちに魔方陣の問題をやらせたら、５方陣の問題を３時間の時間をかけて全員が解いてしまったという。途中にヒントを教えようとしたり、答えを教えようとしたが、子どもたちをそれを制して、問題を考え続けたという。何という粘り強さであろうか。学力不振生徒たちは、このような体験をほとんど持っていない。成功体験をあまり持ち合わせていなのだ。それに対して、知的優秀児達はたくさん持っている。だから、より強く粘ることができる。苦労して頂上に何度も上り詰めて、頂上から見るすばらしい景観を何度も味わったことがあるためである。景観は苦労が多かったらならば、よりすばらしいものとなる。苦労して頂上をきわめた体験が少ない学力不振生徒たちは、粘ることができない。わからなければ、彼らは２、３分も考えないのである。すぐに放り投げてしまう。だから、物事は粘り強く挑戦しなければならないことを教えなければならないのである。「わからないからやらなかった」という言葉を私の前で言ったならば、生徒は大変激怒されることになる。私は徹底的に最初にしつけをする。「わからないから聞かない。」ではなく「聞かないからわからない。」というふうに因果関係が逆であることを徹底的に指導するのである。「１、２回聞いてわかることなら、君たちはわざわざ学校に来ることなどない。理解することは、生みの苦しみと同じような苦しみがある。だが、苦しんだからこそ理解したときの喜びも大きいのだ。」私が口癖のように言う言葉である。生徒の実態にあった授業をしたためだけで、前奏曲に書いた教室の状態が実現したわけではないのである。生徒の実態にあった授業は、生徒に聞かせるための必要条件であって、十分条件ではない。必要十分条件にするためには、実態にあった授業に厳しいしつけを加えなければならないのである。
８章 再び結論
結論をまとめておこう。生徒は本質的に数学が好きである。小学校や中学校の算数教育や数学教育によって嫌いにさせられているが、正しい指導をすれば必ず生徒は数学が好きになるのである。しかも、基礎の欠けている彼らの指導は高校数学から始められるべきのである。その際に、特別の動機付けなどしなくても良いのである。たとえば、魔方陣などから始める必要はないのである。まず徹底的なしつけをする事が必要である。そして教科書の内容を指導すればよいのである。もちろん教科書の内容を指導すると言っても、教科書の内容をその通りにやるという意味ではない。教科書は、生徒にとって簡単な内容から難しい内容へとは構成されていないし、また飛躍も大きい。したがって、生徒の視点に立った再構成が必要なのである。そして基礎への還帰は必要に応じて行えば良いのである。学力不振生徒の最大の問題点が忘却である以上、体系的な基礎への還帰は意味がないのである。単元の学習に必要な範囲で、復習をすれば良いのである。生徒の目の高さにたった指導をしていけば、必ず生徒は数学が好きになるのである。生徒の感想をいくつか載せておこう。
「わかりやすい授業だったから数学が好きになった。」（男子生徒）「高校にはいるまで数学が嫌いだったのに今ではとても好きになりました。それはきっとＹＹ先生だから好きになれたのだと思います。とっても授業の教え方がうまくわかりやすい授業でした。」（女子生徒）「私は、中学のとき数学は得意じゃなかったです。だけど先生が言ったとおり今は数学が好きです。」（女子生徒）「僕は中学の時から数学が苦手で、テストでは余りよい点数がとれませんでした。またそのせいかもしれませんが、数学の教科は嫌いでした。しかし、高校に入ってからは数学が好きになりました。」（男子生徒）「私は、中学の時から数学が嫌いでしたが、なぜか数学がとてもおもしろい教科であるというのが、今、分かりました。今まで、前向きに勉強してもあまり分からなかったのですが、高校の数学は違っていました。なぜか、頭の中に中に入ってくる事柄を忘れることなくすべて自分のものにできてしまうのです。そこで数学に対する気持ちが変わってきたのだと思います。数学はおもしろい教科なのでこれからも苦手意識を持たずにがんばっていこうと思います。」（男子生徒）「中学校の時はほんと数学と聞いただけで嫌でした。でも高校に入学してＹＹ先生に数学を教わるにつれて数学がとてもおもしろいことにきずかされました。たぶん私は数学から逃げていたのかもしれません。でも今数学が好きって言えるようになりました。感謝の気持ちでいっぱいです。ありがとうございました。」（女子生徒）「私はこんなに数学が楽しくできるのは初めてです。すごく数学が嫌いだったのにこんなに数学が好きなったのも初めての経験です。先生が前に言ったこと”君たちは必ず数学が好きになる”は本当ですね。また先生の授業を受けたいです。」（女子生徒）
底辺校と言われる高校の生徒に高校数学を教授することは可能であるし、やならければならないのである。もちろん先にも書いたとおり、低学力生徒たちの特徴は忘却である。したがって、１度定着した学力もやがては消失してしまうであろう。それでは教育に意味がないであろうか。だが、私は問いたい。職員室の先生方ではたして何人の先生が、３乗の展開公式がいえるであろうか。私だって、ＸＸ高校の期末の日本史のテストの問題に答えることはできない。学生時代得意にしていたにも関わらずである。遅かれ早かれ忘却は誰にもくることである。しかしながら、生徒は自信という大きな財産を手に入れたのである。また、物事には粘り強く挑戦しなければならないということを学んだのである。勉強の方法についても彼らは学ぶことができたのである。生徒が社会にでたときに、いろいろなことを勉強していかなければならない。例えば、パソコンやワープロの勉強などをしなければならないが、そのときに小ステップなどで勉強したことは、大いに役立つに違いないのである。数学を学ぶ意義は何であろうか。私は、勉強の仕方を学び、思考の枠組みを広げることであると思う。そういう意味で是非とも生徒に高校数学を学ばせたいのである。
あとがき
この原稿は、昨年校内の研究紀要に発表したものを基に、加筆修正してできたものである。実はこの校内の研究紀要の中でも、論文に仕立て上げ県の研究紀要に投稿予定であると予告しておきながら、放ったらかしておいたものである。全く予想外のことであったが、校内の研究紀要が校外において好評をいただいたのである。あちらこちらで、お褒めの言葉をいただいたのである。友人の強い勧めもあり、今回県の研究紀要に投稿させていただくことにしたものである。
１９９４年ＺＺ県高教研数学部会投稿
VC++講義へ
VB講義基礎へ
VB講義トップへ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座
