第3話 完全数探索プログラム
解答コード例
import java.io.*;
class k{
static int n,cn=0;
public static void main(String args[])throws IOException{
BufferedReader q=new BufferedReader(new InputStreamReader(System.in));
System.out.println("探索範囲を入力してください。");
System.out.print ("探索は=");
n=Integer.parseInt(q.readLine());
f();
}
public static void f(){
int i;
for(i=2;i<=n;i++){
if(g(i)){
System.out.print (i + " ");
if(cn>0 && cn%20==0)System.out.println();
cn++;
}
}
}
public static boolean g(int a){
int i,ks=1,w=0;
int[] h=new int[100000];
h[0]=1;
for(i=2;i<=a/2;i++){
if(a%i==0){
h[ks]=i;
ks++;
}
}
for(i=0;i<ks;i++)w+=h[i];
if(w==a)return(true); else return(false);
}
}
実行例
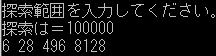
10万まで探索して4つです。
実は、次の完全数は33550336というととてつもない数になります。
次は友愛数の探索プログラムを考えます。
友愛数とは、自分自身を除く約数の和が相手の数と等しくなる自然数の組をいいます。
例えば、220と284です。
220の自分自身を除く約数は、1,2,4,5,10,11,20,22,44,55,110
でその和は1+2+4+5+10+11+20+22+44+55+110=284
284の自分自身を除く約数は、1,2,4,71,142
でその和は1+2+4+71+142=220
で確かに自分自身を除く約数の和が相手と等しくなっています。
では、皆さん挑戦しましょう。
尚、完全数と友愛数の話題は、第1回本屋大賞を受賞した『博士の愛した数式』(小川洋子著)に載っています。
大変面白い小説なので、興味がありましたら一読してみてください。
第2話へ 第4話へ

VB講義へ
VB講義基礎へ
vc++講義へ第1部へ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座
初心者のための世界で一番わかりやすいVBA入門講義(基礎から応用まで)
初心者のための VC++による C言語 入門 C++ 入門 基礎から応用まで第1部
初心者のための VC++による C言語 入門 C++ 入門 基礎から応用まで第2部
初心者のための VC++による C言語 入門 C++ 入門 基礎から応用まで第3部