・・・
すべての場合を考えて、その中で魔方陣の条件を満たすものを拾いコンソールに表示させようとするものです。
3次魔方陣の場合、すべての場合の数は9!=9×8×7×6×5×4×3×2×1=362880通りになります。
4次魔方陣の場合は、16!=16×15×14×・・・×3×2×1=20922789888000通りと信じられない場合の数になります。
この力業ではさすがのコンピュータで4次魔方陣が限界です。
4次魔方陣でさえ、全部の計算が終わるまで30分ぐらいはかかるでしょう。
プログラムはどうしたらよいでしょうか。冒頭だけ書いてみましょう。
#include<iostream>
using namespace std;
int a[3][3],cn;
void f();
int main(){
int i1,i2,i3,i4,i5,i6,i7,i8,i1,i9cn;
cn=0;
for(i1=1;i1<10;i1++){
a[0][0]=i1;
if(a[0][1]!=a[0][0]){
for(i2=1;i1<10;i1++){
a[0][1]=i2;
if(a[0][2]!=a[0][0] && a[0][2]!=a[0][1] ){
for(i2=1;i2<10;i2++){
a[0][2]=i3;
if(a[1][0]!=a[0][0] && a[1][0]!=a[0][1] && a[1][0]!=a[0][2]){
if(a[0][0]+a[0][1]+a[0][2]==15){
for(i4=1;i4<10;i4++){
・
・
・
}
//関数fはコンソールへの表示専用関数
void f(){
int i,j;
for(i=0;i<3;i++){
for(j=0;j<3;j++){
・
・
}
}
}
さて、この気の遠くなるようなコーティングに挑戦して、
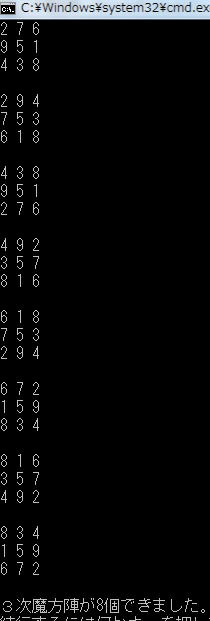
是非とも3次魔方陣すべてを生成させましょう。
第12講第8話へ 第2話へ
