第16講 関数の再帰的呼び出しによる魔方陣の作成
第6話 普遍版魔方陣自動生成プログラムコード解説その3
コード再掲
#include<iostream>
using namespace std;
using namespace System;
void f1(int g);
void f2();
int n,cn;
int a[10][10];
int main(){
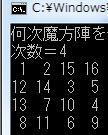
cout<<"何次魔方陣を作成させるのかキーボードから入力してください。"<<endl;
cout<<"次数=";
scanf("%d",&n);
DateTime^ hj=DateTime::Now;
cn=0;
f1(0);
cout<<n<<"次魔方陣が"<<cn<<"個できました。"<<endl;
DateTime^ ow=DateTime::Now;
TimeSpan sa=ow->Subtract(*hj);
cout<<"計算時間は"<<sa.TotalSeconds<<"秒です。"<<endl;
}
void f1(int g){
int i,j,h,w,x,y;
y=g/n;
x=g%n;
for(i=1;i<n*n+1;i++){
a[y][x]=i;
h=1;
if(g>0){
for(j=0;j<g;j++){
if(a[y][x]==a[j/n][j%n]){
h=0;
break;
}
}
}
if(h==1 && x==n-1){
w=0;
for(j=0;j<n;j++){
w+=a[y][j];
}
if(w!=n*(n*n+1)/2)h=0;
}
if(h==1 && y==n-1){
w=0;
for(j=0;j<n;j++){
w+=a[j][x];
}
if(w!=n*(n*n+1)/2)h=0;
}
if(h==1 && y==n-1 && x==0){
w=0;
for(j=0;j<n;j++){
w+=a[j][n-1-j];
}
if(w!=n*(n*n+1)/2)h=0;
}
if(h==1 && y==n-1 && x==n-1){
w=0;
for(j=0;j<n;j++){
w+=a[j][j];
}
if(w!=n*(n*n+1)/2)h=0;
}
if(h==1){
if(g+1<n*n){
f1(g+1);
}
else{
cn++;
f2();
//if(cn==100)break;
}
}
//if(cn==100)break;
}
}
void f2(){
int i,j;
for(i=0;i<n;i++){
for(j=0;j<n;j++){
if(a[i][j]<10)cout<<" "<<a[i][j]<<" ";
if(a[i][j]>=10)cout<<a[i][j]<<" ";
}
cout<<endl;
}
cout<<endl;
}
解説
| 0 | 1 | 2 | 3 | |
| 0 | 1 | 2 | 3 | 4 |
は行合計検査
if(h==1 && x==n-1){
w=0;
for(j=0;j<n;j++){
w+=a[y][j];
}
if(w!=n*(n*n+1)/2)h=0;
}
を受けますが、結果は悲惨なものです。
1+2+3+4=10
ですから、4×(4×4+1)÷2=34に遙かにとどかないわけです。
人形たちは、重複検査と行合計検査という厳しい条件のもと苦戦を強いられ、
3番目と4番目の人形は何度も生成・消滅を繰り返しながら、
| 0 | 1 | 2 | 3 | |
| 0 | 1 | 2 | 15 | 16 |
の時点にいたってはじめて行合計検査をクリアして、
| 0 | 1 | 2 | 3 | |
| 0 | 1 | 2 | 15 | 16 |
| 1 |
へとコマを進めるのです。つまり、5番目の人形がはじめて発生するのです。
2行目においても人形たちは、厳しい戦いを強いられ数え切れないぐらいの生成消滅を繰り返して
| 0 | 1 | 2 | 3 | |
| 0 | 1 | 2 | 15 | 16 |
| 1 | 3 | 4 | 13 | 14 |
に至って、やっと
3+4+13+14=34
を達成します。3行目においても同様な厳しい戦いで苦戦しながら、ようやく
| 0 | 1 | 2 | 3 | |
| 0 | 1 | 2 | 15 | 16 |
| 1 | 3 | 4 | 13 | 14 |
| 2 | 5 | 6 | 11 | 12 |
において5+6+11+12=34を達成して、
| 0 | 1 | 2 | 3 | |
| 0 | 1 | 2 | 15 | 16 |
| 1 | 3 | 4 | 13 | 14 |
| 2 | 5 | 6 | 11 | 12 |
| 3 |
に至るわけですが、重複検査をすべてクリアしても
| 0 | 1 | 2 | 3 | |
| 0 | 1 | 2 | 15 | 16 |
| 1 | 3 | 4 | 13 | 14 |
| 2 | 5 | 6 | 11 | 12 |
| 3 | 7 |
難関である列合計検査
if(h==1 && y==n-1){
w=0;
for(j=0;j<n;j++){
w+=a[j][x];
}
if(w!=n*(n*n+1)/2)h=0;
}
をクリアできません。
1+3+5+7=16
ですから、気が遠くなるほど先が遠いことがわかります。
人形たちはさらに逆対角線、3つの列、対角線、最後の行という6個の合計検査をクリアしなければならないのです。
しかし、人形たちは何の不平不満をこぼさず生成消滅を繰り返しながら働き続けやがてすべての条件をクリアする
| 0 | 1 | 2 | 3 | |
| 0 | 1 | 2 | 15 | 16 |
| 1 | 12 | 14 | 3 | 5 |
| 2 | 13 | 7 | 10 | 4 |
| 3 | 8 | 11 | 6 | 9 |
を発見しコンソールに打ち出すのです。

以下のトレースは是非ご自分で試みてください。
さて、この講は閉めて講を変え普遍版魔方陣自動生成プログラムの高速化を図ります。
C言語 C++講義第1部へ
VB講義へ
VB講義基礎へ
vc++講義へ第1部へ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座
初心者のための世界で一番わかりやすいVBA入門講義(基礎から応用まで)