第1話 円周率の計算方法
第37講は、第36講の継続講です。
したがって、第36講を読んでおくことが必須条件です。
第36講には、☆☆を付けておいたので読んでいらっしゃると思いますが、
もし、読んでいませんでしたら是非お読みください。
初心者にも簡単にできるマルチスレッドですし、
Windowsの特徴を活かし、複数のソフトをナビゲーションソフトから立ち上げるのは魅力的ではないでしょうか。
ですので、☆☆とさせていただきました。
さて、第36講にはまだ達成していない課題があります。
円周率計算ソフトの実装です。
円周率の計算自体が、コンピュータの性能を測る目安として使われてきましたし、
プログラマーにとって大変魅力的なテーマであるということがご存じでしょう。
円周率は、ウィキペディアによると「2011年現在では、円周率は小数点以下10兆桁まで計算されている。」
そうです。
そして、求め方も様々あるようです。
http://ja.wikipedia.org/wiki/%E5%86%86%E5%91%A8%E7%8E%87を参照していただければと思います。
また、あっしーのぺーじのπのページにも歴史や求め方などが載っていますので、興味がある方はお読みになってください。
ここでは、このページのπ/4=arctan 1 の級数展開に掲載されている
「ライプニッツ(Gottfried.W.Leibniz ; 1646-1716)の公式 π/4=atn(1)=1-1/3+1/5-1/7+1/9-1/11+・・・」
を採用してみたいと思います。
for文と使いループ回数を増やせば増やすほど、近似値は精度を増していきます。
Form5を
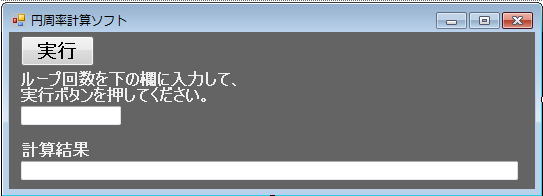
として、実行のコードを考えてみましょう。
参考まで、ウィキペディアからπを引用しておきましょう。
