第９講　関数の再帰的使用

第６話　関数の再帰的使用による順列の作成
Form1

縦は長めにとってください。また、Form1のプロパティの配置のAoutoScroll

はTrueにしておいてください。例えば、７次順列は５０４０個の順列があるからです。
幾らForm1を長めにとっても、入りきらないのでスクロールできるようにしておくわけです。

コーティング例
#pragma once
#include<stdlib.h>
namespace 順列作成 {
　　　　　　・
　　　　　　・
　　　　　　・
#pragma endregion
　　 private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
　　　　　　　　　　　int n;
　　　　　　　　　　　int *a;
　　　　　　　　　　　long s=0;

　　　　　　　　　　　dataGridView1->Rows->Clear();

　　　　　　　　　　　n=int::Parse(textBox1->Text);
　　　　　　　　　　　a=(int* )malloc(4*n);
　　　　　　　　　　　s=f(0,n,a,s);
　　　　　　　　　　　dataGridView1->Rows->Add();
　　　　　　　　　　　dataGridView1[12,s+1]->Value =s.ToString();
　　　　　　　　}
　　　　　　　　long f(int g,int n,int* a,long s){
　　　　　　　　　　　int i,j,h;
　　　　　　　　　　　for(i=1;i<n+1;i++){
　　　　　　　　　　　　　a[g]=i;
　　　　　　　　　　　　　h=1;
　　　　　　　　　　　　　if(g>0){
　　　　　　　　　　　　　　　for(j=0;j<g;j++){
　　　　　　　　　　　　　　　　　if(a[g]==a[j]){
　　　　　　　　　　　　　　　　　　　h=0;
　　　　　　　　　　　　　　　　　　　break;
　　　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　}
　　　　　　　　　　　　　if(h==1){
　　　　　　　　　　　　　　　if(g+1<n){
　　　　　　　　　　　　　　　　　s=f(g+1,n,a,s);
　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　　　else{
　　　　　　　　　　　　　　　　　dataGridView1->Rows->Add();
　　　　　　　　　　　　　　　　　for(j=0;j<n;j++){
　　　　　　　　　　　　　　　　　　　dataGridView1[j,s]->Value =a[j];
　　　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　　　　　s++;
　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　}
　　　　　　　　　　　}
　　　　　　　　　　　return s;
　　　　　　　　　}
};
}

拍子抜けするほど簡単です。
これで、7次であろうと12次であろうとできてしまうのです。
理論的は、何次でもできるコーティングなのです。実行例を示しましょう。

　　　　　　　　　　　　　　　　　　・
　　　　　　　　　　　　　　　　　　・
　　　　　　　　　　　　　　　　　　・

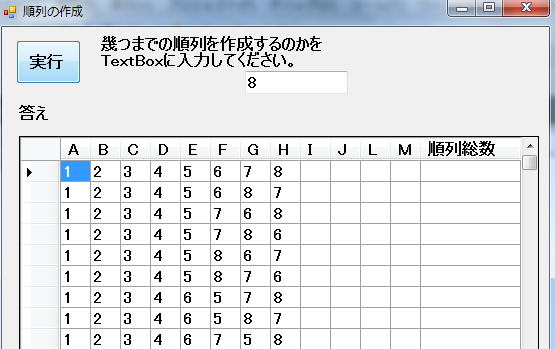
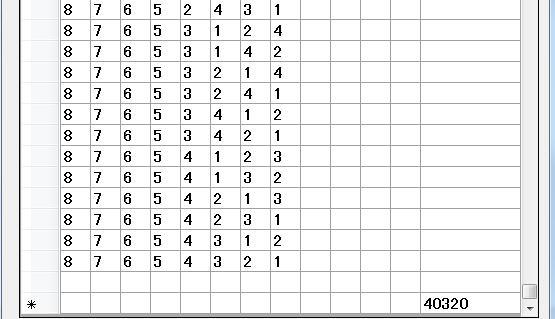
とてもコーティングする気になりませんが、もしfor文版なら９次元ループです。
大変複雑になります。
それに対して、自己再帰版は至ってシンプルです。

それでは、解説に入りますが、今回も３次順列を例にとって説明します。
例えば８次順列では、トレースが膨大になってしまうからです。
プログラムコードを読む際に大切なことは、各変数の役割をしっかり把握することでしたね。
このコードではセル番号はgです。前のfor文に対応させてlでもよかったわけですが、
私が初めて作った魔方陣作成プログラムは、C言語によるものでした。
プログラムで作らせた魔方陣をディスプレイ（モニター）に表示させていたので、
画面位置のつもりでgとしていたのです。
以来、VBA等でもたくさん魔方陣作成プログラムを作ってきましたが、
ずっとgで通してきました。
魔方陣の場合セルは２次元ですが、２次元は１次元で表現できることは前に学習しました。
２次元セルを１次元番号gで整理するというアイディアは、私の魔方陣作成研究において、
もっとも誇りにもっているもののひとつです。
魔方陣作成も、結局今挑戦している順列作成と原理的に同じであると気がついたことによって、
私の魔方陣研究は、爆発的に進展することになったのです。
そして、このアイディアは間違いなく時間割作成にも生かせます。
時間割作成は、２次元セルで縦横の条件があるという点で、
魔方陣作成とまったく同じであるからです。
半年ぐらい缶詰で研究開発の時間があれば、
完全な時間割作成ソフトができると思っています。
完全なというのは、市販されている時間割ソフトは例外なく出来が悪く、
かえって手で組んだ方が速い場合もあるぐらいです。
時間割ソフトで組めたとしても出来が悪すぎて、
結局時間割係の先生方が、何日も缶詰作業で手直しているのが現状です。
私は、いろいろと仕事ややりたいことがたくさんありますので、
時間割作成ソフトの開発に携わるつもりはありません。
やりたいことは、今行っている講座もひとつですが、
左脳一辺倒になっている現在の数学教育を根底からひっくり返すこと、
社会科学の方法について私の説を証明すること、
の２つも入ります。
この２つは、私のライフワークであると思っています。
そのほかの小さな夢としては、現在の数独問題作成ソフトVer.1を改良し、
より高速に、より難度が高い良問を作成できるようにすることもあります。

ごめんなさい。少し脱線しました。
ソフトハウスの方は、是非私の魔方陣作成ソフトを利用して完全な時間割ソフト開発していただければと思います。

さて、脱線は終了して解説に戻りましょう。
gはセル番号です。
for(i=1;i<n+1;i++)のiが各セルに入る数字です。
前のfor文版では、３次配列の３に対応して３次元でｉ，ｊ，ｋが用意されましたが、
関数の再帰的使用においては、１つでよいです。
理由は、関数f(0,n,a,s)、f(1,n,a,s)、f(2,n,a,s)は入れ子式人形のそれぞれ異なる人形です。
セル番号gが異なれば、同じfでも次元の違う関数なのです。
セル番号0なら、１次元目のループ、セル番号1なら２次元目のループ、セル番号2なら３次元目のループ
というわけです。ですから、for(i=1;i<n+1;i++)のi1つで済むのです。
1つでセル番号gに応じて何次元ループでも可能なのです。

f(0,n,a,s)、f(g+1,n,a,s)の引数と戻り値について説明しましょう。
引数nは、ｎ次配列のｎです。aは、ポインタです。渡された関数fでは、要素数ｎの１次元配列として働きます。
sは順列総数を数える変数です。総数を数える変数はカウンタ変数と呼ばれます。

各変数の役回りが明確になったところで、トレースしてみましょう。
もう一度確認しますが３次順列で説明しますのでn=3です。
まず、
　　　　　　　　　　　s=f(0,n,a,s);
でg=0、n=3、s=0で関数fが呼び出されます。
n=3なので、

対象セルは３つです。関数fの１次元ループが
　　　　　　　　　　　for(i=1;i<n+1;i++){
１次元目ループ（セル番号０のループ）になります。
まず、１巡目でa[g]=i; から、

が実現します。
g=0ですから、条件
　　　　　　　　　　　　　h=1;
　　　　　　　　　　　　　if(g>0){
　　　　　　　　　　　　　　　for(j=0;j<g;j++){
　　　　　　　　　　　　　　　　　if(a[g]==a[j]){
　　　　　　　　　　　　　　　　　　　h=0;
　　　　　　　　　　　　　　　　　　　break;
　　　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　}
はあっさりクリアして、
　　　　　　　　　　　　　if(h==1){
　　　　　　　　　　　　　　　if(g+1<n){
　　　　　　　　　　　　　　　　　s=f(g+1,n,a,s);
　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　　　else{
　　　　　　　　　　　　　　　　　dataGridView1->Rows->Add();
　　　　　　　　　　　　　　　　　for(j=0;j<n;j++){
　　　　　　　　　　　　　　　　　　　dataGridView1[j,s]->Value =a[j];
　　　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　　　　　s++;
　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　}
が実行されます。g+1<nは1<3で条件を満たしますので、if文が実行されf(g+1,n,a,s);によって、fが再帰的に呼び出されます。
fが自分自身を呼び出しています。ただし、呼び出しているfはf(0,n,a,s)であるのに対して、呼び出されるfはf(1,n,a,s)です。
他の引数は、とりあえず無視して表示するとf(0)とf(1)
（n、a、sをグローバル変数にすればこうなります。今回はローカルにしてあるのでn、a、sを引き渡しています。
gが次元を決定する役割を担っています。
n、a、sはグローバル変数にすれば無視できるのでこれからは簡略にf(0)等と表現することにします。）
です。入れ子式人形の、一番外側の人形がf(0)で、外側から２番目の人形がf(1)です。
つまり、入れ子式人形の一番外側の人形が外から２番目の人形を呼び出しているのです。
さて、f(1)の次元は

セル番号１の世界

です。
f(1)の
for(i=1;i<n+1;i++){
によって

となります。そして、
　　　　　　　　　　　　　h=1;
　　　　　　　　　　　　　if(g>0){
　　　　　　　　　　　　　　　for(j=0;j<g;j++){
　　　　　　　　　　　　　　　　　if(a[g]==a[j]){
　　　　　　　　　　　　　　　　　　　h=0;
　　　　　　　　　　　　　　　　　　　break;
　　　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　}
によって、１と１が比較され内容が同じなのでh=0となり、
　　　　　　　　　　　　　if(h==1){
　　　　　　　　　　　　　　　if(g+1<n){
　　　　　　　　　　　　　　　　　s=f(g+1,n,a,s);
　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　　　else{
　　　　　　　　　　　　　　　　　dataGridView1->Rows->Add();
　　　　　　　　　　　　　　　　　for(j=0;j<n;j++){
　　　　　　　　　　　　　　　　　　　dataGridView1[j,s]->Value =a[j];
　　　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　　　　　s++;
　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　}
は実行されず、f(1)のループの２巡目になり、

今回は条件
　　　　　　　　　　　　　h=1;
　　　　　　　　　　　　　if(g>0){
　　　　　　　　　　　　　　　for(j=0;j<g;j++){
　　　　　　　　　　　　　　　　　if(a[g]==a[j]){
　　　　　　　　　　　　　　　　　　　h=0;
　　　　　　　　　　　　　　　　　　　break;
　　　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　}
をクリアして、
　　　　　　　　　　　　　if(h==1){
　　　　　　　　　　　　　　　if(g+1<n){
　　　　　　　　　　　　　　　　　s=f(g+1,n,a,s);
　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　　　else{
　　　　　　　　　　　　　　　　　dataGridView1->Rows->Add();
　　　　　　　　　　　　　　　　　for(j=0;j<n;j++){
　　　　　　　　　　　　　　　　　　　dataGridView1[j,s]->Value =a[j];
　　　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　　　　　s++;
　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　}
が実行されます。
g+1<nは、2<3なのでs=f(g+1,n,a,s);が実行されf(2)が呼び出されます。
つまり、f(1)がf(2)を呼び出したのです。f(2)によって、セル番号２の世界

に入ります。言い換えれば、入れ子式人形の最後の人形の世界になります。

f(2)の
for(i=1;i<n+1;i++){
によって

となります。g=2なので、if文
　　　　　　　　　　　　　h=1;
　　　　　　　　　　　　　if(g>0){
　　　　　　　　　　　　　　　for(j=0;j<g;j++){
　　　　　　　　　　　　　　　　　if(a[g]==a[j]){
　　　　　　　　　　　　　　　　　　　h=0;
　　　　　　　　　　　　　　　　　　　break;
　　　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　}
が実行され、for文の1巡目によって、１と１の比較がなされますが、内容が同じで
h=0となり、for文は強制的に終了となります。
したがって、
　　　　　　　　　　　　　if(h==1){
　　　　　　　　　　　　　　　if(g+1<n){
　　　　　　　　　　　　　　　　　s=f(g+1,n,a,s);
　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　　　else{
　　　　　　　　　　　　　　　　　dataGridView1->Rows->Add();
　　　　　　　　　　　　　　　　　for(j=0;j<n;j++){
　　　　　　　　　　　　　　　　　　　dataGridView1[j,s]->Value =a[j];
　　　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　　　　　s++;
　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　}
は実行されず、f(2)の2巡目になり、

で
　　　　　　　　　　　　　h=1;
　　　　　　　　　　　　　if(g>0){
　　　　　　　　　　　　　　　for(j=0;j<g;j++){
　　　　　　　　　　　　　　　　　if(a[g]==a[j]){
　　　　　　　　　　　　　　　　　　　h=0;
　　　　　　　　　　　　　　　　　　　break;
　　　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　}
の1巡目は１と２の比較でクリアしますが、２巡目において２と２の比較になり、内容が同じで
h=0となってしまい、
　　　　　　　　　　　　　if(h==1){
　　　　　　　　　　　　　　　if(g+1<n){
　　　　　　　　　　　　　　　　　s=f(g+1,n,a,s);
　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　　　else{
　　　　　　　　　　　　　　　　　dataGridView1->Rows->Add();
　　　　　　　　　　　　　　　　　for(j=0;j<n;j++){
　　　　　　　　　　　　　　　　　　　dataGridView1[j,s]->Value =a[j];
　　　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　　　　　s++;
　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　}
再び実行されず、f(2)の３巡目になり、

となります。今度は、
　　　　　　　　　　　　　h=1;
　　　　　　　　　　　　　if(g>0){
　　　　　　　　　　　　　　　for(j=0;j<g;j++){
　　　　　　　　　　　　　　　　　if(a[g]==a[j]){
　　　　　　　　　　　　　　　　　　　h=0;
　　　　　　　　　　　　　　　　　　　break;
　　　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　}
の1巡目、２巡目において１と３、２と３が比較されますがいずれも内容が違っていて、
hは１のまま書き換えられず、
　　　　　　　　　　　　　if(h==1){
　　　　　　　　　　　　　　　if(g+1<n){
　　　　　　　　　　　　　　　　　s=f(g+1,n,a,s);
　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　　　else{
　　　　　　　　　　　　　　　　　dataGridView1->Rows->Add();
　　　　　　　　　　　　　　　　　for(j=0;j<n;j++){
　　　　　　　　　　　　　　　　　　　dataGridView1[j,s]->Value =a[j];
　　　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　　　　　s++;
　　　　　　　　　　　　　　　}
　　　　　　　　　　　　　}
が実行されますが、g+1<nは3<3で正しくないので、if文の方は実行されずelse文が実行され、
1個目の順列がデータグリッドビューに表示され、s++;によって順列総数が１とされます。

解説が大分長くなりましたので以後のトレースは次話で。
次話で第９講は終了といたします。
次話が終わればいよいよ卒業研究と卒業試験を残すのみとなります。
卒業に向けてがんばりましょう。





第５話へ　第７話へ

vc++講義へ
vb講義へ
ＶＢ講義基礎へ
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座へ

数学研究室に戻る