Form1
第９講 関数の再帰的使用
第３話 順列の作成
Form1
個数がｎ個のときの順列をｎ次順列と呼ぶことにします。
まず、３次順列のコード例は次のようになります。
#pragma endregion
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^
e) {
int i,j,k,l,h1,h2;
int *a;
long s=0;
dataGridView1->Rows->Clear();
a=(int* )malloc(12);
for(i=1;i<4;i++){
a[0]=i;
for(j=1;j<4;j++){
a[1]=j;
h1=1;
if(a[0]==a[1])h1=0;
if(h1==1){
for(k=1;k<4;k++){
a[2]=k;
h2=1;
for(l=0;l<2;l++){
if(a[l]==a[2]){
h2=0;
break;
}
}
if(h2==1){
dataGridView1->Rows->Add();
for(l=0;l<3;l++){
dataGridView1[l,s]->Value =a[l];
}
s++;
}
}
}
}
}
dataGridView1->Rows->Add();
dataGridView1[12,s+1]->Value =s.ToString();
}
};
}
実行結果
すでにこのコードを見ただけで、頭が爆発しそうです。
大変難解です。
解説は、次話で詳しく行うとして
４次順列を続けて掲載しましょう。
４次順列
#pragma endregion
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^
e) {
int i,j,k,l,m,h1,h2,h3;
int *a;
long s=0;
dataGridView1->Rows->Clear();
a=(int* )malloc(16);
for(i=1;i<5;i++){
a[0]=i;
for(j=1;j<5;j++){
a[1]=j;
h1=1;
if(a[0]==a[1])h1=0;
if(h1==1){
for(k=1;k<5;k++){
a[2]=k;
h2=1;
for(l=0;l<2;l++){
if(a[l]==a[2]){
h2=0;
break;
}
}
if(h2==1){
for(l=1;l<5;l++){
a[3]=l;
h3=1;
for(m=0;m<3;m++){
if(a[m]==a[3]){
h3=0;
break;
}
}
if(h3==1){
dataGridView1->Rows->Add();
for(m=0;m<4;m++){
dataGridView1[m,s]->Value =a[m];
}
s++;
}
}
}
}
}
}
}
dataGridView1->Rows->Add();
dataGridView1[12,s+1]->Value =s.ToString();
}
};
}
実行結果
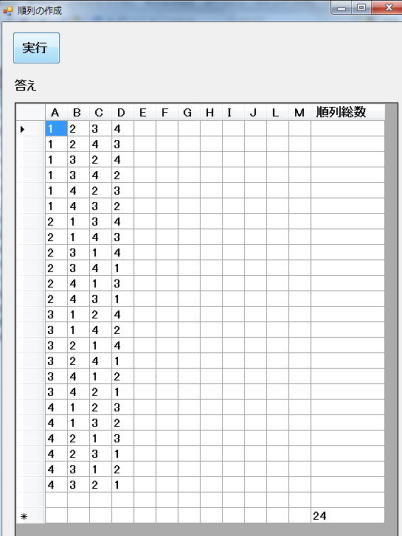
以上から、関数の自己再帰を使わないと５次、６次、７次になる相当困難であることを感じ取っていただければと思います。
関数の自己再帰であれば、たったひとつのプログラミングで一般化が可能です。
つまり、理論的には１００次であろうと１０００００次であろうと計算可能なわけです。
ただ、２０１０年購入時において最高のスペックを誇っていた私のパソコンでも８次おいてすでに１９秒の計算時間がかかりますので、
１００次を計算させるとするとどのぐらいかかるか見当もつきませんが。
というのは概算で、９次なら１９×９＝１７１秒、１０次なら１７１×１０＝１７１０秒と階乗に比例する単位で計算時間が増えていくからです。
ですから現実的でないとはいえますが、理論的には１００次であろうと１０００００次であろうと可能なわけです。
それに対して、for文版の方は一般性がないのでいちいちプログラムコードを書き換えなければなりません。
そして、手間が信じられないほどかかります。
４次順列で５次元ループになりますから、１２次配列ならなんと１３次元ループになってしまいます。
逆に自己再帰型の場合は、コードをいちいち書き換えないで何万次元であろうと理論的には可能なのです。
如何に自己再帰型が優れているかわかります。
第２話へ 第４話へ
vc++講義へ
vb講義へ
ＶＢ講義基礎へ
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座へ
