複数の引数による等差数列の和コード例
Private Sub CommandButton1_Click()
Dim h As Long, o As Long, b As Long
h = Cells(5, 2)
o = Cells(6, 2)
b = Cells(7, 2)
Cells(8, 2) = f(h, o, b)
End Sub
Function f(h As Long, o As Long, b As Long)
Dim w As Long, i As Long
w = 0
For i = h To o Step b
w = w + i
Next
f = w
End Function
Private Sub CommandButton2_Click()
Columns("B").Select
Selection.ClearContents
Cells(1, 1).Select
End Sub
実行例
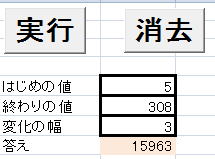
次は、円の一部の面積を求める計算を考えます。
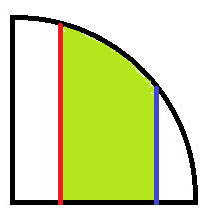
指定するのは、半径、x軸と赤の交点、ｘ軸と青の交点です。
要するに、半径と積分範囲の始めと終わりを引数にして、面積を計算させたいわけです。
この面積を計算させるためには
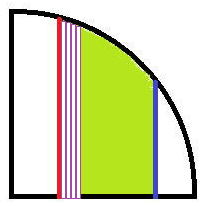小さい長方形に分けて、その面積を加えていけば求められます。半径ｒ円の方程式は、
です。
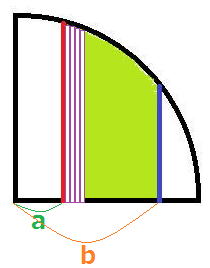
始まりをａ、終わりのｂとし、小さい長方形の横をｄ（例えば１０００個の長方形に分ければ、ｄ＝（ｂ−ａ）／１０００）とすると、
長方形の面積は、
何個の長方形に分割するかによって、面積の精度が異なります。
分割個数を増やせば増やすほど、面積の精度が高く（つまり、誤差が小さく）なります。
そこで、分割個数ｋも引数とします。
このときは、もちろんｄ＝（ｂ−ａ）／ｋです。
したがって、面積を求めるFuncitonプロシージャfは、f(r,a,b,k)として呼び出すことにします。
そして、ｒ，ａ，ｂ，ｋの値はシートから入力するものとします。
さらに、精度を調べるため ｒ＝１，ａ＝０，ｂ＝１の場合の面積の４倍も、求める面積の下に表示させるものとします。
ｒ＝１，ａ＝０，ｂ＝１の場合の面積の４倍は、半径１の面積に相当しπになります。
したがって、πの近似値を求めさせていることになります。
分割個数をｋを大きくすると、πに近づいていきます。
大変難しい課題になってしまって申し訳ありませんが、是非挑戦して下さい。
