第２５講　フィボナッチ数列と黄金比
第１話　フィボナッチ数列とは？

皆さんは、ダ・ヴィンチ・コードの映画をご覧になりましたか。
あるいは、原作の方をお読みになっているでしょうか。
コードは暗号の意味です。
ですから、いろいろな暗号が原作や映画には出てきます。
究極の暗号は、暗号解読官のソフィー・ヌヴーその人であった･･･
種明かしになってしまいますので、それ以上には触れないことにしましょう。

映画の最初の方に出てくる暗号があります。
１１２３５８１３２１
でしたでしょうか。
暗号解読官のソフィー・ヌヴーは、この暗号が実はフィボナッチ数列であることを看破して物語が進んでいくのです。
みなさん、数列の規則性がわかりますか。
１，１，２，３，５，８，１３，２１，・・・
この数列がフィボナッチ数列です。

答えは、例によって３０行下に示しましょう。






















答え
前の２つの項の和がその項になるです。
１＋１＝２
１＋２＝３
２＋３＝５
３＋５＝８
５＋８＝１３
８＋１３＝２１
　　　・
　　　・
　　　・
このフィボナッチ数列は、数列をanとするとan＋１／anが黄金比なることが知られています。
黄金比とは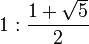です。
黄金比とは、いろいろなところに出てきます。
A4用紙の縦横の比、人間と足の長さと胴の長さの比、パルテノン神殿、ひまわり、バラ、オーム貝
自然界の至る所に黄金比が登場するのです。
パルテノン神殿から予想できるように、美術作品も黄金比になっているものが数多くあるといいます。

何故なのか。それはフィボナッチ数列を見ていただければわかります。
そうです。
入れ子式構造です。
入れ子式構造とは、自然の究極の秘密であると私は思っています。

さて、入れ子式構造に注目してフィボナッチ数列を作ってみましょう。
入れ子式ですから、もちろんプロシージャの再帰的利用で実現できます。

第２５講第７話へ　第２話へ

　　


VBA講義第１部へ
vc++講義へ
vb講義へ
ＶＢ講義基礎へ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座へ
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座へ

数学研究室に戻る