 が表示され3回目の3巡目ループが終わり、
が表示され3回目の3巡目ループが終わり、2巡目のループのNextにより
第10講 Subプロシージャの再帰的使用理解のための課題
第5話 ループ版の詳しいトレースその3
Private Sub CommandButton1_Click()
Dim a(2) As Integer
Dim i As Integer, j As Integer, k As Integer, l As Integer, cn As Integer
Dim h1 As Byte, h2 As Byte
cn = 0
For i = 1 To 3
a(0) = i
For j = 1 To 3
a(1) = j
h1 = 1
If a(1) = a(0) Then h1 = 0
If h1 = 1 Then
For k = 1 To 3
a(2) = k
h2 = 1
For l = 0 To 1
If a(2) = a(l) Then
h2 = 0
Exit For
End If
Next
If h2 = 1 Then
For l = 0 To 2
Cells(5 + 2 * Int(cn / 3), 1 + 4 * (cn Mod 3) + l) = a(l)
Next
cn = cn + 1
End If
Next
End If
Next
Next
Cells(5 + 2 * Int(cn / 3), 1) = "順列総数"
Cells(5 + 2 * Int(cn / 3), 4) = cn
End Sub
| 0 | 1 | 2 |
| 2 | 1 | 3 |
3つめの順列 が表示され3回目の3巡目ループが終わり、
が表示され3回目の3巡目ループが終わり、
2巡目のループのNextにより
ⅱ j=2となります。
| 0 | 1 | 2 |
| 2 | 2 | k |
これはチェック
h1 = 1
If a(1) = a(0) Then h1 = 0
抵触し、
If h1 = 1 Then
For k = 1 To 3
a(2) = k
h2 = 1
For l = 0 To 1
If a(2) = a(l) Then
h2 = 0
Exit For
End If
Next
If h2 = 1 Then
For l = 0 To 2
Cells(5 + 2 * Int(cn / 3), 1 + 4 * (cn Mod 3) + l) = a(l)
Next
cn = cn + 1
End If
Next
End If
は実行されず、Nextにより
ⅲ j=3となります。
| 0 | 1 | 2 |
| 2 | 3 | k |
これはチェック
h1 = 1
If a(1) = a(0) Then h1 = 0
をクリアし
If h1 = 1 Then
For k = 1 To 3
a(2) = k
h2 = 1
For l = 0 To 1
If a(2) = a(l) Then
h2 = 0
Exit For
End If
Next
If h2 = 1 Then
For l = 0 To 2
Cells(5 + 2 * Int(cn / 3), 1 + 4 * (cn Mod 3) + l) = a(l)
Next
cn = cn + 1
End If
Next
End If
が実行され、4回目の3巡目ループに入ります。
① k=1のとき、
| 0 | 1 | 2 |
| 2 | 3 | 1 |
h2 = 1
For l = 0 To 1
If a(2) = a(l) Then
h2 = 0
Exit For
End If
Next
2回ともクリアして
If h2 = 1 Then
For l = 0 To 2
Cells(5 + 2 * Int(cn / 3), 1 + 4 * (cn Mod 3) + l) = a(l)
Next
cn = cn + 1
End If
によって、4個目の順列 が表示され、カウンタcnも4となります。
が表示され、カウンタcnも4となります。
4回目の3巡目のNextによって、
② k=2となり
| 0 | 1 | 2 |
| 2 | 3 | 2 |
これは
h2 = 1
For l = 0 To 1
If a(2) = a(l) Then
h2 = 0
Exit For
End If
Next
の1回目のループでチェックされてしまい、
If h2 = 1 Then
For l = 0 To 2
Cells(5 + 2 * Int(cn / 3), 1 + 4 * (cn Mod 3) + l) = a(l)
Next
cn = cn + 1
End If
は行われず、Nextにより
② k=3となり
| 0 | 1 | 2 |
| 2 | 3 | 3 |
今度は
h2 = 1
For l = 0 To 1
If a(2) = a(l) Then
h2 = 0
Exit For
End If
Next
の2回目のループでチェックされてしまい、
If h2 = 1 Then
For l = 0 To 2
Cells(5 + 2 * Int(cn / 3), 1 + 4 * (cn Mod 3) + l) = a(l)
Next
cn = cn + 1
End If
は実施されません。これで4回目の3巡目ループが終了して、続いて2回目の2巡目ループも終了して、
Ⅲ i=3の場合となります。
| 0 | 1 | 2 |
| 3 | j | k |
すぐに、3回目の2巡目ループに入り
ⅰ j=1から
| 0 | 1 | 2 |
| 3 | 1 | k |
となりますが、これは
h1 = 1
If a(1) = a(0) Then h1 = 0
をクリアして
If h1 = 1 Then
For k = 1 To 3
a(2) = k
h2 = 1
For l = 0 To 1
If a(2) = a(l) Then
h2 = 0
Exit For
End If
Next
If h2 = 1 Then
For l = 0 To 2
Cells(5 + 2 * Int(cn / 3), 1 + 4 * (cn Mod 3) + l) = a(l)
Next
cn = cn + 1
End If
Next
End If
が行われ、5回目の3巡目ループに入ります。
① k=1のとき、
| 0 | 1 | 2 |
| 3 | 1 | 1 |
For l = 0 To 1
If a(2) = a(l) Then
h2 = 0
Exit For
End If
Next
2回目のチェックをクリアできず
If h2 = 1 Then
For l = 0 To 2
Cells(5 + 2 * Int(cn / 3), 1 + 4 * (cn Mod 3) + l) = a(l)
Next
cn = cn + 1
End If
は実行されず、Nextにより
② k=2となり、
| 0 | 1 | 2 |
| 3 | 1 | 2 |
これは
For l = 0 To 1
If a(2) = a(l) Then
h2 = 0
Exit For
End If
Next
を問題なくクリアして、
If h2 = 1 Then
For l = 0 To 2
Cells(5 + 2 * Int(cn / 3), 1 + 4 * (cn Mod 3) + l) = a(l)
Next
cn = cn + 1
End If
によって、5個目の順列 が表示され、順列総数cnも5となります。次に、
が表示され、順列総数cnも5となります。次に、
③ k=3から
| 0 | 1 | 2 |
| 3 | 1 | 3 |
となりますが、
For l = 0 To 1
If a(2) = a(l) Then
h2 = 0
Exit For
End If
Next
1回目に引っかかり、
If h2 = 1 Then
For l = 0 To 2
Cells(5 + 2 * Int(cn / 3), 1 + 4 * (cn Mod 3) + l) = a(l)
Next
cn = cn + 1
End If
実行されず、5回目の3巡目ループが終了して、3回目の2巡目ループは
ⅱ j=2となります。
| 0 | 1 | 2 |
| 3 | 2 | k |
h1 = 1
If a(1) = a(0) Then h1 = 0
をクリアして
If h1 = 1 Then
For k = 1 To 3
a(2) = k
h2 = 1
For l = 0 To 1
If a(2) = a(l) Then
h2 = 0
Exit For
End If
Next
If h2 = 1 Then
For l = 0 To 2
Cells(5 + 2 * Int(cn / 3), 1 + 4 * (cn Mod 3) + l) = a(l)
Next
cn = cn + 1
End If
Next
End If
6回目の3巡目ループに入ります。
① k=1のとき、
| 0 | 1 | 2 |
| 3 | 2 | 1 |
For l = 0 To 1
If a(2) = a(l) Then
h2 = 0
Exit For
End If
Next
2回ともチェックをクリアして
If h2 = 1 Then
For l = 0 To 2
Cells(5 + 2 * Int(cn / 3), 1 + 4 * (cn Mod 3) + l) = a(l)
Next
cn = cn + 1
End If
から、6個目の順列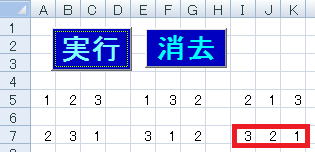 が表示され、cn=6となります。
が表示され、cn=6となります。
② k=2のとき、
| 0 | 1 | 2 |
| 3 | 2 | 2 |
For l = 0 To 1
If a(2) = a(l) Then
h2 = 0
Exit For
End If
Next
の2回目に抵触して
If h2 = 1 Then
For l = 0 To 2
Cells(5 + 2 * Int(cn / 3), 1 + 4 * (cn Mod 3) + l) = a(l)
Next
cn = cn + 1
End If
は実施されず、
② k=3
| 0 | 1 | 2 |
| 3 | 2 | 3 |
となりますが、これは
For l = 0 To 1
If a(2) = a(l) Then
h2 = 0
Exit For
End If
Next
の1回目にチェックされ、
If h2 = 1 Then
For l = 0 To 2
Cells(5 + 2 * Int(cn / 3), 1 + 4 * (cn Mod 3) + l) = a(l)
Next
cn = cn + 1
End If
は行われず、6回目の3巡目のループが終了して、
ⅱ j=3となります。
| 0 | 1 | 2 |
| 3 | 3 | k |
これは
h1 = 1
If a(1) = a(0) Then h1 = 0
をクリアせず
If h1 = 1 Then
For k = 1 To 3
a(2) = k
h2 = 1
For l = 0 To 1
If a(2) = a(l) Then
h2 = 0
Exit For
End If
Next
If h2 = 1 Then
For l = 0 To 2
Cells(5 + 2 * Int(cn / 3), 1 + 4 * (cn Mod 3) + l) = a(l)
Next
cn = cn + 1
End If
Next
End If
は実施されず、3回目の2巡目ループも終了となり、1巡目ループも続いて終了していよいよ3次元ループが終了です。
最後、
Cells(5 + 2 * Int(cn / 3), 1) = "順列総数"
Cells(5 + 2 * Int(cn / 3), 4) = cn
によって、順列総数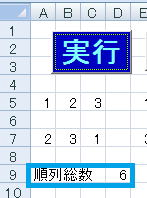 が表示されプログラムは終わります。
が表示されプログラムは終わります。
本当に長いトレースお付き合いいただき、ありがとうございます。
トレースは大変重要です。すべての場合において、詳しくトレースする必要はありません。
直観で明瞭に大丈夫だと思えばトレースはしなくてもよい場合もあります。
しかし、思う結果が得られなかったり、ほんの少しでも不明瞭の部分があるなら、今回のように粘り強くトレースをする必要があります。
ぜは、皆さん今回のトレースを参考に8次順列12345678のすべての生成に挑戦しましょう。
生成という言葉に、インスピレーションを感じませんでしたか。
例えば、9次順列を応用すれば、3次魔方陣の自動生成に挑戦できることに気がついたでしょうか。
もちろん、ループ版では次元が変わる度に別のコードを用意しなければなりませんので、
一般性=汎用性のあるプログラムはかけませんが、8次順列ループ版の次に学ぶSubプロシージャの再帰的使用を使えば、
たったひとつの短いコードでいかなる次元にも対応できるプログラミングが可能です。
Subプロシージャの再帰的使用を使えば、魔方陣の自動生成が可能なばかりか、汎用性のあるプログラムが可能なのです。
魔方陣普遍超高速版を開いていただくと、

となりますが、K3には3以上26以下の整数を自由に入れることが出来ます。汎用性があると、ひとつだけでなくいろいろな場合
(今回の場合は、3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26が可能)
に対応出来るということです。理論的には、26の上限は必要ありません。それ以上だと処理速度が遅くなるので、上限を26としているだけです。
2次魔方陣は存在しませんし、1次魔方陣は意味がありませんので、可能な意味のある魔方陣ということでは制限がないのです。
普遍性があるのです。普遍性のあるプログラムを汎用性のあるプログラムといいます。
もちろん、今回の順列作成は数独問題自動生成にも応用できます。
ですから、粘り強く8次順列ループ版の作成に取り組みましょう。
ただし、シートは次のように変更してください。
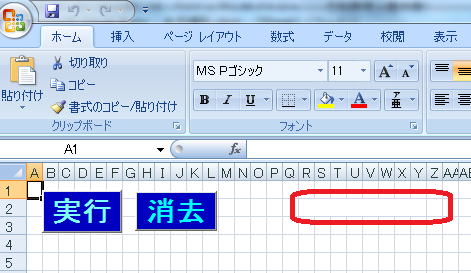 赤い囲いのところに、総数を表示させます。
赤い囲いのところに、総数を表示させます。
理由は、8次順列だと40320通りもありセルが小さいと表示できないので、赤い囲いは結合してあります。

やり方は、R2からZ2までをドラッグで選択し、右クリック→セルの書式設定→配置タブ→セルを結合するにチェックを入れます。
コード
Cells(5 + 2 * Int(cn / 3), 1) = "順列総数"
Cells(5 + 2 * Int(cn / 3), 4) = cn
も適宜変更してください。
第4話へ 第6話へ

vc++講義へ
vb講義へ
VB講義基礎へ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座へ
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座へ
数学研究室に戻る