「直観のない形式は空虚であり、形式のない内容は混沌である。」(カント)
私が以下に述べる問題意識をもつようになったのは、実に小学5年生のときにまで遡る。したがって、30年間疑問をもっていた問題について、語ろうとしているわけだ。問題意識の要点は、現在の数学教育は、極端に論理に偏っていて、直観やイメージがあまりにも軽視されている、ということである。すなわち、左脳に偏った右脳を使わない数学になっているということである。創造の源泉は、右脳にあるといわれていることを考えれば、由々しき問題であるといわざるを得ない。
先進国でありながら、米国や欧州に比べて、ノーベル賞の受賞者が極端に少ない要因の一つが、ここにあるのではないだろうか。数学の発展をはじめとして、諸科学の発展のためには、右脳と左脳をバランスよく協同させることが必要である。物理学者や数学者にも論理的なタイプと直観的なタイプがいるということが事実であるとしても、いずれのタイプにおいても論理と直観を協同させていることは、おそらく疑いのないことである。将棋や囲碁においても、一流の棋士は読みと勘を備えている。NHKのある番組によると、将棋史上において初めて全冠(7冠)を果たした羽生は他の棋士に比べて右脳をフルに使っているという。羽生の強さの秘訣はここにある。論理を支える土台は、直観である。直観をそして右脳を働かせることが肝要なのである。
小学生が中学生になったとき、最初に抱く疑問の一つは数学と算数はどう違うのかということである。ところが中学生を納得させられる説明を、指導者はすることができない。理由は簡単である。現在の算数はまったく数学と変わるところがないからである。現在の算数は、完全に数学化している。もっとも私は、歴史を紐解いたことがないので、現在という言葉が正しいかどうかは確信を持っているわけではわけではない。したがって、少なくとも現在の算数はといっておこう。
私が小学5年生のときに抱いた疑問は、担任の先生が割合や速さの問題の解法を説明するときに、なぜ公式を使って説明するのだろか、ということであった。私からすると、かけ算になるのかわり算になるのかは、意味を考えれば自明なことなので、公式など必要としないものだった。だから、公式など覚えたことがなかった。(自慢話でなく後論のため必要なことなので、述べておくと、公式を覚えなくても私は算数の成績はクラスで常にトップであった。)私は、公式など覚えさせ公式で解くより、意味に戻って説明するべきであると思っていた。だから、担任の先生が自慢げに、あたかも自分の創意工夫であるか様に(これが彼の創作でないことは、後にいろいろな先生が常に自慢げにこの図を書いたことから知ることになる。)、次の図を示したときは、あきれ返ったものである。
にこにこマーク
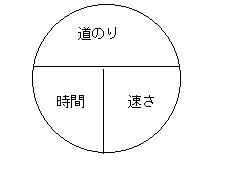
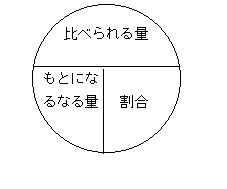
この図は、形式化の極限に属するものである。意味は完全に蒸発している。公式による教育を、公式主義と呼ぶとすれば、公式主義の究極ともいうべきものである。イメージなき衣である。カントの言葉を借りれば、内容のない形式である。しかし、この過ちはそのときの担任の先生の責任ではない。なぜならどの指導者も、同じ指導法をとっているからである。日本の算数教育が、公式に偏った教育をしているのである。本来必要としない公式を、算数に密輸入してしまったのである。
なぜ指導者たちが、指導をするときに公式に頼るのか。一つの原因は、指導者の発想が左脳的で、それが良き指導であると思いこんでいるからである。だが、もっとも大きな要因は、公式による指導を児童が歓迎するからである。意味からの指導は、幼児期から左脳化されている児童には、理解することが困難なのである。だから、ほとんどの児童は2時間で8キロの道のりを進むときの速さは、8÷2という計算で求められることを直観的に把握することができないのである。なぜわり算になるのか、という本質的な部分を抜きにして、そこから逃げ出す指導が公式なのである。意味を剥奪された公式は、丸暗記される運命にある。そして丸暗記するための方法として、ますます空虚になった先の「にこにこマーク」のようなものが考え出されるのである。(いろいろな指導者が自慢げに語る「にこにこマーク」は愚の骨頂である。)電卓の仕組みを知らなくても、計算ができるように速さや割合について本質的には理解していなくても、計算できてしまう方法こそが公式による理解なのである。
問題は算数教育にだけにあるのではない。数学教育にも同様な問題がある。比重からいえば、算数に比べれば数学は、論理的であり公式主義的である。つまり一度証明されたものを、定理や公式として認め、必要がない限りは理由や起源にはふれず、定理や公式を前提として問題にあたる、ということになっているのである。場面によっては、公式を証明できなくても、使い方さえ知っていれば、事足りるのである。だから、公式の証明をいっさいしない授業もあり得るのである。実際に明治時代の帝国大学の工学部で、そういう指導法をとった外国人教授もいたという。私も前々任校において、同様な指導法をとった。前任校や本校においても、習熟別のクラスよっては同様な指導をしている。
しかし、数学においても論理だけでなく直観も大切である。数学には確かに公式化・形式化が必要である。形式化するためには、具体的なもの(直観的なもの)を抽象する必要がある。だが、抽象とは具体的なものを捨象することではない。抽象とは、具体的なものの括弧入れである。抽象された形式は、具体的なものを内包しているのでなければならない。記号や公式の背後にはというより、その内には意味やイメージがあるのでなければならない。物理学者は例外なく、記号の背後にあるイメージをとらえることが大切であると強調する。理論物理学者が微分方程式を操作しているとき、理論物理学者の頭脳にはイメージがありありと浮かんでいる。イメージなき数学操作をするとき、物理学者は現実・自然から遠ざかってしまう。物理学科の中にも素養のないものがいて、空虚な数学操作をして、突拍子ようもない結論を出したりする。たとえば、相対性原理である光より速い物質は存在しない、という仮定は不自然なので、光より速い物質の存在を仮定する超相対性理論を講じたりするのである。事実と理論が転倒し倒錯してしまっている。はじめに事実や現実があるべきなのに抽象的で内容のない理念が先行してしまっている。数学においても、よき研究者であるためには、論理とともに直観を作動させなければならない。
三角関数は、三角比を抽象して一般化して定義される。だが、角度の制限が90度未満のときには、三角比に一致する。三角比は、歴史的にいえば古代エジプトにおいてナイルの氾濫のために土地の区画がわからなくなるために、研究されたものである。起源からして実践的であり、内容的にも直角三角形に結びついていて、具体的である。三角比を普遍化して、三角関数を導いたとしても直角三角形のイメージが背後にあるのでなければならない。
数学の教科書の構成は、歴史的なものを完全には排除していないため、具体的なものを辛うじて維持している。だが、単元の内容には行き過ぎた形式化が随所にみられる。そして何よりも、指導者の指導が問題である。公式を証明するや否や、公式を使う例題の説明に入り、演習にはいる。これの繰り返しによって、数学の授業は構成されている。ここではイメージを喚起するような教育はなされない。たとえば、PならばQが正しいとき、QをPであるための必要条件、PをQであるための十分条件、逆も成立するときお互いに必要十分条件という、と説明してすぐに例題にはいる。そして、必要条件、十分条件、必要十分条件の判定法を機械的に説明するのである。本来から言えば、ここの説明で大事なことは、なぜ必要という言葉が使われ、また十分という言葉が使われるかと言うことである。だが、私の想像ではここの説明をする指導者はほとんどいない。だから、必要条件や十分条件の意味を本当に理解している生徒は、形式的な説明から内容を読みとることのできる生徒だけである。それはほんの一握りの生徒だけだ。ここで大切なことは、直観による理解なのである。
しかし、直観による数学教育というのは、非常に困難な道である。なぜなら教育全般が左脳に偏った教育になっていて、児童生徒の発想が左脳的になってしまっているからである。意味からの指導は、児童生徒を混乱に陥れる。右脳的な立場からの指導が軌道に乗るためには、組織的にして忍耐強い指導が必要であると思われる。左脳に慣らされた児童生徒の頭脳を少しずつ右脳的な発想へと変えていかなければならない。理解を急がせないことが肝要だ。理解できないとき、安易な道を児童生徒は求める。これに妥協してはならない。公式による理解は真の理解ではない。理解は茨の道であること知らしめなければならない。いろいろな数学者が、証明の個々の論証を追えたとしても、すなわち論理的に自分で説明できたとしても、理解したとは思えないと、語っている。数学者にとって大事なことは、論証全体を直観的に理解することなのである。児童生徒の理解も論理のレベルから直観の領域に高めなければならないのである。
そして、何よりも我々が考える道を困難にしているものは、右脳的発想に基づく算数数学教育の研究の歴史がない、という点である。私が30年も前にもった問題意識であるのにも関わらず、私の実践は失敗の歴史であった(もちろん成功例も小数ながらあるからこそこの小論があるのである。)、というのが正直なところであり、また、私と同一の問題意識をもった指導者は、私の知る範囲ではいないである。以下の論考を読んで、1人でも多くの賛同者が現れ、直観数学教育の研究をそして実践を共にしていく方が現れることを切に願うと同時に、才能あふれる共鳴者が研究を発展させ、算数数学教育を変革していくに違いない、ということを確信するものである。


