数学はイメージだ!
最初に、私の掲げる直観算数および直観数学のイメージをつかんでもらうために、私の実践においてもっとも成功した例を挙げたいと思う。対数の指導である。私の前々任校は、俗に教育困難校とか底辺校と言われる学校であった。ある年の合格者の数学の平均点は23点であり、15点以下のものが1/3に達したことがある。したがって、毎年一桁台の生徒が多数入学してくる高校であった。なかには5−2+3を0と答える生徒もいたのである。一昔前ある工業高校の生徒が分数の計算ができないということで、話題になったことがあるが、教育困難校といわれる高校においては、分数の計算は難しい計算であるということは常識なのである。したがって、前々任校における数学指導は、困難を極めた。そして、生徒が理解できない代表的な章の1つが、指数・対数なのである。特に後半の対数は抽象度が高く、生徒たちにとって理解困難なものであった。私が、指導で困った例題の1つが、次の問題である。

したがって、常用対数表からX≒1.25
この数式の操作の下にどんなイメージが隠されているか、読みとれるだろうか。指導者が潜在しているイメージを紐解いてあげない限り、ほとんどの生徒は読みとることは不可能である。前々任校の生徒たちでは100%不可能である。私の想像では、今これを読んでいる先生方でさえ、読みとるのは困難であるのではないだろうか。私自身これをさっと読んだとき、すぐには理解した気持ちにはなれなかった。もちろん個々の展開は追うことができたし、また、何もみないで生徒たちに説明することはできた。しかし、何か腑に落ちないものがあったのである。そうだ、直観的理解ができていないのだ。
私は、直観的に生徒たちに理解させる方法を模索した。試行錯誤を重ねた結果、指数・対数の章は次のように指導することにした。
導入 ある中学生の発見 1時間
展開 教科書の指導 15時間
まとめ 対数の意味 1時間(先の例題の説明)
この指導によって、前々任校のほとんどの生徒たちが、対数のイメージを掴み、先の例題を解けるようになった。「数学ってこんなに奥が深いのか」という感想を書いた女子生徒もいた。また、1年間の授業の最後に書いてもらう感想文に、もっとも感動した章として、「指数・対数」をあげていた生徒もいた。私事になるが、ほとんどの生徒が先の例題を解けるようになったことがあまりにも嬉しくて、こう指導したらうまくいったんだ、という話を妻(妻は国語科の高校教員である。)にしたら、「高校時代対数って、少しも意味が分からなかったけど、この説明で対数のイメージがよくつかめた。私も高校時代にこういう先生に巡り会えたら、数学を好きになっていたかもしれない。」といわれた、ということを付け加えさせていただきたい。
また、今年の前任校の校内研究授業において、対数の意味の部分を扱い校長先生をはじめとして、いろいろな先生から御教示をいただいた。研究授業自体は、内容を欲張りすぎ2時間分を1時間のなかに詰め込んでしまったので、失敗であったが、研究授業の後の授業研究で、授業の問題点をご指摘いただき大変参考になった。ここで学んだ点を含めて、指導展開例を評述してみたいと思う。
導入 ある中学生の発見 1時間
展開 教科書の指導 15時間
まとめ 対数の意味(1) 1時間(簡易計算機の作成)
対数の意味(2) 1時間(先の例題の説明)
問題演習 2時間
以下の記述は、導入と対数の意味(2)は前々任校における実践を基にしたノンフィクションであり、対数の意味(1)の方は、前任校における研究授業を参考にはしているが、フィクションである。
導入 ある中学生の発見 1時間
「今日はある天才中学生について話をする。その中学生が、2年生のときに発見したことについてである。」といって授業を開始する。そして、黒板の左の上の方に大きく2と書く。次に生徒を順番に指名し、今黒板に書いた数字の2倍を次々に言わせ、その数字を右へ右へと書いていく。2,4,8,16,32,・・・ というようにだんだん計算が大変になってくる。これだけで生徒は緊張し計算に没頭し、これからいったい何が起きるのかという期待が教室中に充満してくる。桁数が5、6桁になると、「次私だ。」と生徒は大変緊張しているで、この辺で指名をうち切る。「さて、今計算してもらった数字に今から黄色で番号を打っていく。そうすると不思議なことが起きる。」といって2,4,8,と白チョークで大きく書かれている数字の上に小さく黄色チョークで番号を振っていく。すると以下のような表が完成する。
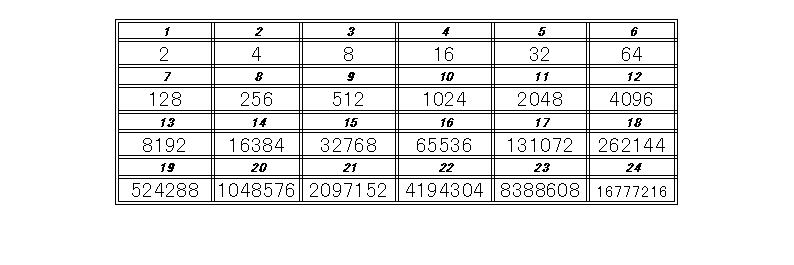
持参した電卓を一番前の生徒に渡して、「先生は普段計算間違ってばかりいるけど、実は暗算の天才だったんだ。」といって以下の計算など5題ぐらいを瞬時に計算し、その計算が正しいことを電卓を渡した生徒に確認させる。
256×16384=4194304
128×8192=1048576
はじめは生徒たちは不思議そうな顔をしているが、4,5題計算していく内に計算原理がわかり、にやにやする生徒が出始める。そして、次にわり算にはいる。
1048576÷512=2048
16777216÷32768=512
わり算ではかけ算の原理がわかっていた生徒は、1,2題で計算方法がわかり、にっこりしている。また、かけ算がわからなかった生徒のなかにも、4,5題わり算を計算していく内にかけ算、わり算の両方の計算方法がわかってくる生徒もかなり出てくる。この段階で累乗算にはいる。
16の5乗 =1048576
8の8乗=16777216
累乗算の計算は、さすがにわかる生徒は少数のようだ。しかし、教室の1/3ぐらいの生徒は、かけ算わり算については、計算原理がわかり他の生徒に小さな声で教え始める。普段は怖い私も、このときは生徒たちが教え合っている姿をにこにこ見ている。頃合いをみて、少年の発見をまとめる。

「つまり黄色の数字(表ではイタリックの小さめの数字)を使えば、かけ算は足し算で、わり算は引き算で、累乗算はかけ算でできることを発見したわけだ。少年はこれを発見したとき、あまりにも不思議でこの表を魔法の表ないしはコンピューターの表と呼んだんだ。」というと、女子生徒からは「かわいい」という声が出る。さらに、私は少年が偉大だった点にふれる。「少年はこの表を喜ぶと共に、すぐに不満を覚える。この表は確かに便利だが、この表に載っている数字以外計算ができない。そこで少年は、表の一般化を考えた。2と4の間には3がある。3にも1と2の間の数で対応する黄色の数字があるはずだ。さらに、4と8の間の5,6,7についても2と3の間の数で、だんだんに大きくなっていく黄色の数が対応しているはずだ。その数を全部見つけてやれば、あらゆるかけ算は足し算で、わり算は引き算で、累乗算はかけ算でできるはずだ。そして、少年はその数字をすべて見つけてやろうと、努力するのである。」だが、中学2年生だった彼にはそれは不可能な課題だった、といって話を次に移す。
黄色の数字(表ではイタリックになっているやや小さめの数字)がこれから学んでいく、対数であることを教える。そして、白色の数字(表ではイタリックになっていないやや大きめの数字)を真数という、いい下のような表を提示する。
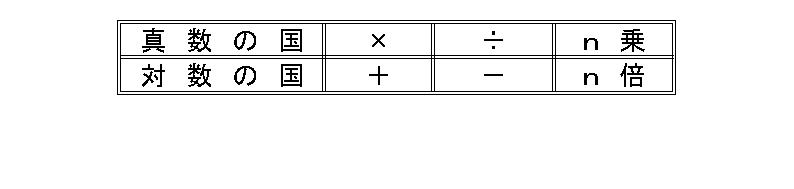
「真数の国と対数の国では、話す単語が違うだけでなく、文法も違うわけだ。そして文法の対応表がこの表というわけさ。」
中学2年生が発見したことは、実は約300年前にすでに発見されていたことを告げる。「発見者はネピアという人である。ネピアといってもティシュペーパーとは何の関係もない。(生徒の笑い)コンピュータのない時代天文学者にとって、膨大な桁数扱う計算は悩みの種だった。しかし、ネピアが対数の表を作ってくれたおかげで、天文学者の寿命は延びたと言うことだ。」
こうして1時間の授業を終えるわけだが、もちろん授業の最後には「ところで、その天才中学生って誰?」と聞くのを忘れない。見え見えの話なので、おおかたの生徒はにやにやしていて答えない。ところが、間が抜けた生徒が必ずいて、いかにも私は気がついたという感じで「それは先生です。」と答える生徒がいるのである。こうして、私はにっこと笑って、チャイムを聞くのである。