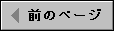ここでの指導は、取り立てて工夫があるわけではない。通常の指導である。ただ、前々任校か前任校または本校かによって、指導時間が違うのはもちろんのことである。前任校や本校においても、習熟度別クラスの違いに応じて、説明の詳しさや問題演習の質と量が変わってくる。前任校や本校でも習熟度の高くないクラスでは、問題演習は教科書のレベルに限定されるべきである。そして、説明は丁寧でなければならない（と言っても本校の場合、習熟度別やコース別の授業でも、クラス内の格差が大きくて、限界がある。学力が上の生徒の要望にも応えてやらなければならないからだ。）。
一般にある誤解を解いておきたい。前々任校では、入試の成績が１５点以下のもので１／３にも達し、分数の計算はもちろんのこと簡単な正負の計算さえできない生徒がクラスに少なからずいた。前々任校では、一般受験では大学でも短大でも合格できる生徒は１人もいなかったし、また期待もできなかったので、指導にはかなりゆとりがある部分があった。前任校や本校のように受験に対応するために、必ず教科書を終わらさなければならないと言うことはなかった。そこで次のような考え方もないわけではない。
「分数の足し算や簡単な正負の計算もできない生徒たちに、あえて高校数学を学ばせなくてもいいのではないか。受験という制約がないなら、基礎のない生徒たちのためにあえて背伸びせず、中学校や小学校の基礎に戻って指導してあげてもいいのではないか。」
実は上の考え方は、大変な誤解なのである。栃木県高教研数学部会の研究紀要に投稿した「数学教育論（学力観のコペルニクス的転回）」（新学力観を参照）に書いたことなので詳しくは書かないが、上の考え方は誤った学力観に基づいているのである。誤った学力観というは以下の考え方である。
「中学で学ぶ数学は小学校で学ぶ算数より難しく、また高校で学ぶ数学は中学校で学ぶ数学より難しい。そして、数学は積み重ねの学問なので、基礎のない生徒に高校数学を学ばせることは難しい。」
そして、むしろ生徒に高校数学を強いるのは指導者の自己満足であるとさえ思う方もいらっしゃるであろう。生徒の学力の構造を知らない、完全な誤解である。標準の学力に達しない生徒たちの学習能力における最大の問題点は、「理解力」ではなく「記憶力」である。彼らは理解したとしても、２０分も自転車を漕いでいるうちに、すべてを忘却してしまうのである。だから、体系的に基礎を学習し直したとしても、なにも残らないのである。
だが、彼らは「理解力」を持っていないわけではない。丁寧に指導すれば、高校数学でも理解できるのである。基礎の不足については、現在の単元の中で必要に応じて補ってあげればいいのである。たとえば、定積分を計算するときには分数の計算が必要になるので、このときに約分や通分などを教えてあげればすむのである。彼らが我々が丁寧に指導してやって、高校数学を理解できたときの喜びは、通常に考えられているより遙かに大きい。私がその場面に最初に遭遇したときにはびっくりするほどであった。理由は簡単である。彼らは小学校中学年以降算数や数学を一度も理解したことがないからである。
詳細については、前稿「数学教育論（学力観のコペルニクス的転回）」（新学力観に収納）を是非読んでいたでいただくことにして、話を本筋に戻そう。右脳数学といっても、左脳を無視するわけではない。はじめに書いたように、左脳と右脳の協同が大切なのである。言い換えると、論理と直観の結合が大切だと言うことである。通常の指導は、直観の部分が抜け落ちて論理に偏った教育になってしまっている、といっているのにすぎないのである。だから右脳数学においても、記号による指導も当然のことながら行われなければならないのである。（ただ、式を変形する操作においてイメージが喚起されるかと言うことを問題にする。物理の指導に比べれば、この部分は非常に軽視されていると言ってよい。）だから、この展開においては、論理的な指導に力点が置かれて行われる。つまり導入においては、直観やイメージに比重が置かれ、展開においては論理中心の指導がなされ、再びまとめにおいて直観を強調して、論理と直観の統合をはかろうという構想なのである。
まとめ
対数の意味(1)（簡易計算器）１時間
ここでは、割り箸を使って計算尺を作らせ、計算尺を使っていろいろな計算をさせた後、どうして計算ができるのかを考えさせる。はじめに導入で使った天才中学生の発見を、印刷しておいて、配布しておく。
天才中学生の発見
「今日はみんなにすばらしいものを作ってもらうぞ。かけ算、わり算ができてしまう不思議な計算器、計算尺の作成だ。材料は高価なものなので、先生のポッケトから出させてもった。材料はこれ（割り箸を見せる。生徒笑い。）だ。総額は１８０円（生徒再び笑い。）。
計算器を作った後、どうして計算ができるのかみんなで考えてみよう。ヒントは今配ったプリントのなかにある。」
用意する材料 割り箸、木材２本（目盛りを打っておく）、プリント
はじめに実際の見本を見せながら作業手順を説明する。「さて、この巨大割り箸をみてごらん（生徒笑い）。この巨大割り箸のようにまず割り箸に等間隔に目盛りを打ってほしい。間隔は自由だが、１ｃｍぐらいが適当だろう。」
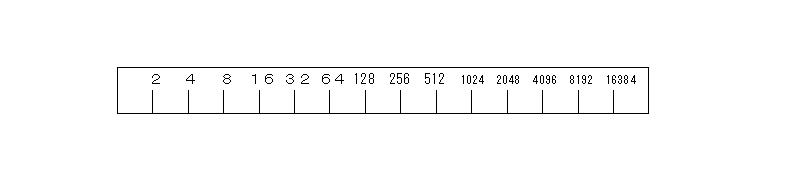目盛り打たせた後、上のように数字を記入させる。もう１本にも同様に、目盛りを打たせ、さらに裏側にも等間隔に目盛りを打たせ、下のように数字を記入させる。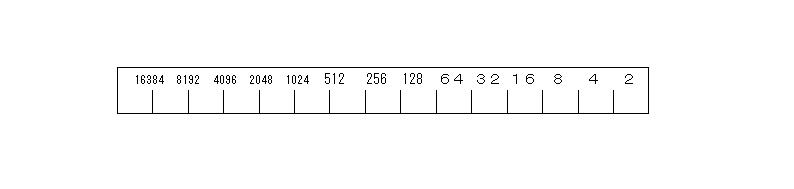
同方向に数字が記入されたものは、割算用に使用され、逆方向に記入されたものはかけ算用に使用される。つまり２本目の割り箸を、表にしたり裏にしたりするとかけ算やわり算ができるのである。表と裏の制作が終わったら、いよいよ簡易計算器による計算ということになる。まだ、制作途中の生徒もいるので、一旦は制作をやめさせ、私の方をみるように指示する。そして、計算の仕方を説明する。かけ算は、１本目と２本目の裏を使い次のよ
うに計算する。たとえば、３２×２５６ならば下図のようにあわせる。
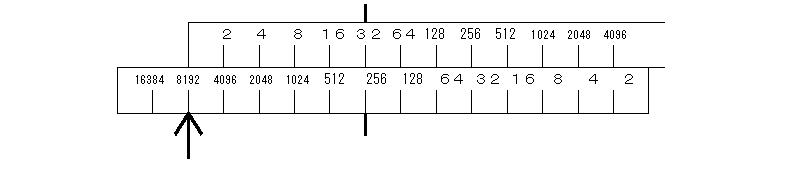
すると左の矢印のところに答え８１９２が出ているのである。「あら不思議なことに一番左に答えが出ているではないか（生徒驚きの表情）。ほかの例で計算しても、必ず答えが出るね。さて、みんなも自分の割り箸を使って、計算してごらん」生徒たちは計算に熱中する。お互いに問題を出し合ったり、筆算で確認したりしながら、生徒は驚きの度を深めている。頃合いをみてわり算の方に入る。「さて、次わり算にはいるからみんないったん作業をやめて先生の方をみてごらん。わり算は、２本目の表を使って計算するよ。巨大割り箸の２本目を反対にひっくり換えして、たとえば１２８と８を合わせると、１２８÷８の答えが一番左側に１６と出ている。その他で計算してもそうだ。今度はみんなが自分の割り箸を使って計算してごらん。割り箸をひっくり返すことを忘れないように。」生徒たちはまた計算に熱中する。生徒たちは感動を深めると同時に、どうして計算できるのかという疑問を深めることになる。
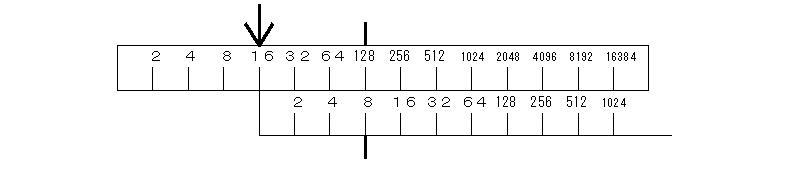
「どうだ、見事にわり算とかけ算ができてしまうだろう。本当に不思議なことだね。どうして、かけ算わり算ができてしまうのか、考えてみよう。ヒントは最初に言ったようにプリント『天才中学生の発見』のなかにある。よく考えてみよう。」
生徒に考えさせる。５分ぐらい時間をおいてから、複数を指名する。正解をいえる生徒がいれば儲けものであるが、１０中８，９は答えられる生徒がいないと考えておいた方がいい。それでもこの考えさせる時間は貴重である。不思議さを深めさせ、印象度を強めると同時に、一生懸命に頭を働かせるからである。このとき生徒たちは、左脳と右脳を協同させながら必死に考えるであろう。現代教育が失ってしまっているものの１つは、この考える時間である。
「そうだね。これは難しい問題だ。だからヒントを与えることにしよう。割り箸の目盛りのところに記入してある数字は、プリントの表のイタリックでない、大きめの数字と同じだ。この数字は真数だった。では表のイタリックになっている小さめの数字すなわち対数は割り箸のどこに隠れているだろうか。」
上記のヒントを与えても、答えられる生徒がいれば、幸運な方である。何人かを指名する。４，５人も指名して答えられなければ、いよいよ指導者側が説明する。
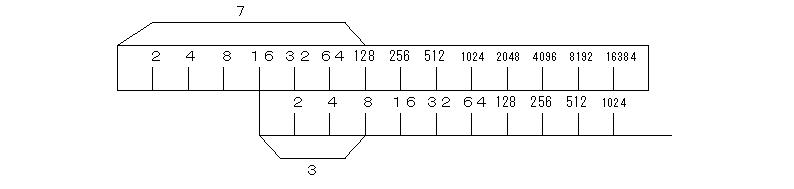
「対数は割り箸の本当の長さだ。たとえば、左から数えて７目盛りのところに１２８という数字がある。みんなの場合は、１目盛り１ｃｍで打ったから左端から７ｃｍのところに１２８があることになる。次に８をみると、８は左から３目盛りのとことにあるから左端から３ｃｍのところにあることになる。」
ここで生徒に考えさせる。２，３分も待つとＡが手を挙げてくれた。「先生、長さの観点で考えたとき、計算尺がやっている計算は、
７−３＝４
という計算です。これは対数の世界における計算です。実際に記入してある数字は、真数の世界の言葉に翻訳した真数です。対数の国での引き算は、真数の国においてはわり算です。だから真数の国で考えたときには、つまり実際に記入してある数字で考えた場合には、わり算になるのです。」
「君は実にすばらしいことに気がつきましたね。あの天才中学生に負けないぐらいの天才的な発見です。君は実に偉い！ワンダフル！実にグット！（生徒笑い）」
７ − ３ ＝ ４ 対数
１２８ ÷ ８ ＝１６ 真数
かけ算でも同様である。つまり実際の長さが対数であり、計算尺では足し算を計算している。それを真数語に翻訳すれば、かけ算ななるというわけだ。
「ここで対数の性質を復習してみよう。対数の性質は、３つあった。いえる人いるかな」
Ｂが手を挙げたので指名する。Ｂに板書させる。
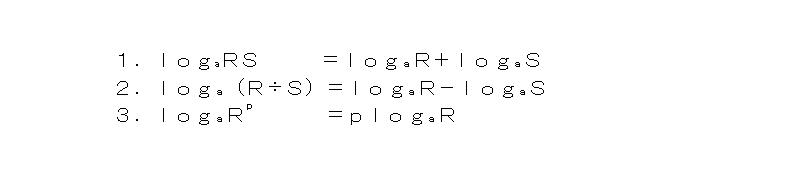
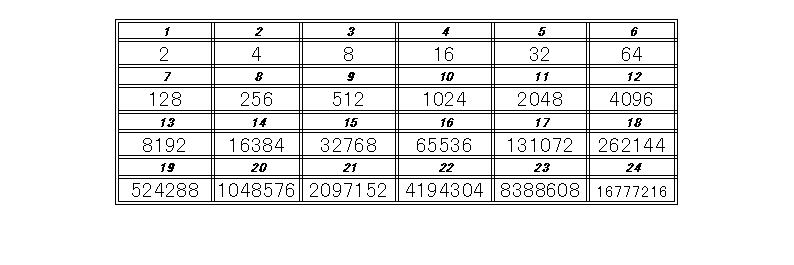
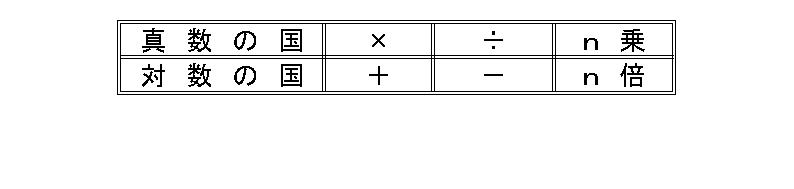
「ここでこの対数の性質の意味を考えてみよう。実はｌｏｇａ は真数の言葉を対数の言葉に翻訳する機械または翻訳しろという命令なんだ。だからｌｏｇａＲは真数Ｒを対数語（ｒとしておこう）に翻訳したものなんだ。ｌｏｇａＳは真数Ｓを対数語（ｓ）に翻訳したものだ。するとｌｏｇaＲＳは真数ＲＳを対数語に翻訳したものということになる。だから公式が意味しているのは、真数の国におけるかけ算は、対数の国では足し算になるということを意味しているということになる。結局３つの公式は、例の中学生が発見したことを式化したものだということになる。つまり２番目の公式は、真数の国のわり算は、対数の国では引き算ということだ。そして３番目の公式は、真数の国でのｐ乗は対数の国ではｐ倍というわけだ。」
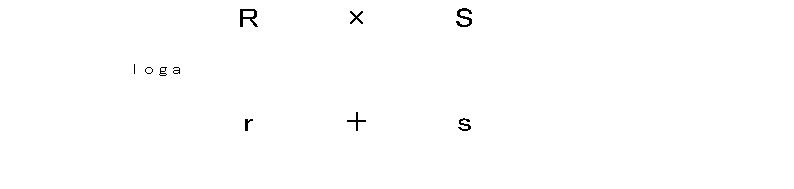
上の図を板書して、まとめとする。次時の予告として公式３の意味を考え、
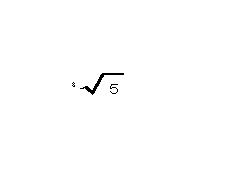
の計算を再度取り上げるという。
