ここでは公式3の意味をもう一度考え、
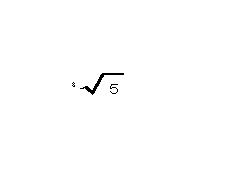
の記号操作の下に隠されていた意味(イメージ)を取り出す、ことを目標にする。最初に前時の復習をする。つまり、対数の3つ性質の意味は、中学生が発見した内容にほかならならない、ことを復習する。
「性質1は、真数の世界でかけ算になるものは、対数の世界では足し算になる、ということを意味している。性質2は、真数の世界でわり算になるものは、対数の世界では引き算になる、ということを意味していた。性質3は、真数の世界でp乗になるものは、対数の世界ではp倍になる、ということを意味していた。今日は性質3に焦点を当てたい。」 そして、次の図を板書する。
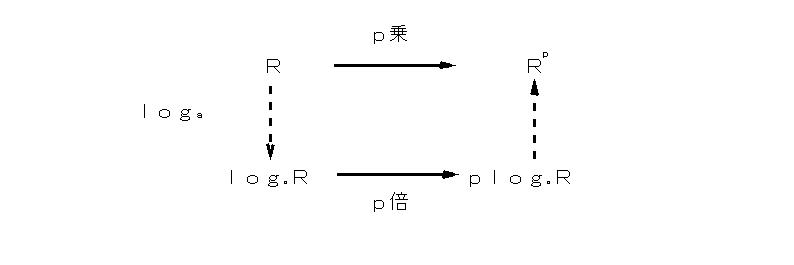
「さて、p101の例14をもう1回復習してみよう。」

したがって、X≒1.25
「今日は、この記号操作の下にどんな意味やイメージが隠されているのか考えてみることにしよう。」
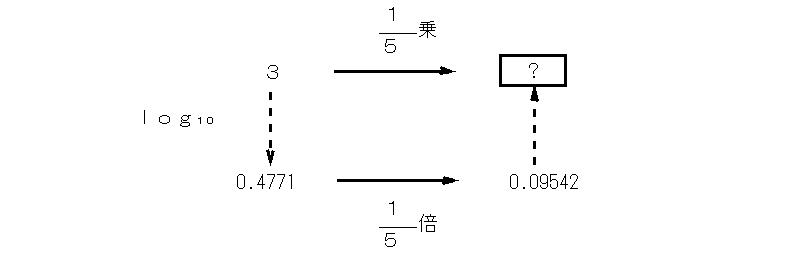
「1行目のlog103という計算では、3という真数語を常用対数語に翻訳するように要求している。実は、常用対数表は真数語から対数語へ翻訳する辞書であったわけだ。常用対数表から真数語の3は対数語では0.4771である。そして、

という計算の各行は、1行目は真数の世界でのp乗は対数の世界では、p倍に相当することをいっている。2行目、3行目では計算して、p倍を出している。ここで再び辞書である常用対数表を利用する。今度は、対数語を真数語に翻訳するので、常用対数表を逆読みする。そして、3の1/5乗は約1.25であるということがわかった、というわけだ。(生徒は、納得顔の生徒とまだ怪訝そうな顔をしている生徒がいる。どんなに筋が通った説明でも、1回で納得し理解することは難しいものである。だから、同じ様な例題で何回か説明し、そして演習することが絶対に不可欠である。この演習なしに理解したという気持ちにはなれないものだ。)3の1/5乗を表面から攻めていったら難攻不落のままであったろう。それを対数の世界に迂回することによって、落城させてしまったというわけだ。急がば回れだ。(生徒笑い。)あるいは玄関のドアは、鍵がかかっていたので、勝手口に回って入り、内側から鍵を開けてしまったようなものだ。(生徒再び笑い。)数学にも泥棒と同じ様な知恵が必要なんだ。(生徒笑い。)迂路を得ることによって、秘密の扉はこじ開けられたのだ。」
この後、いくつかの類題を生徒に解かせる。
類題
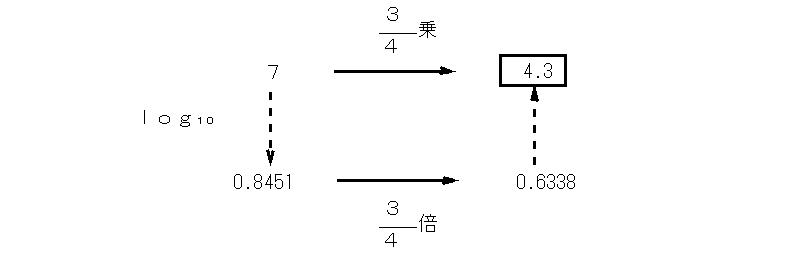
Ⅰの解答
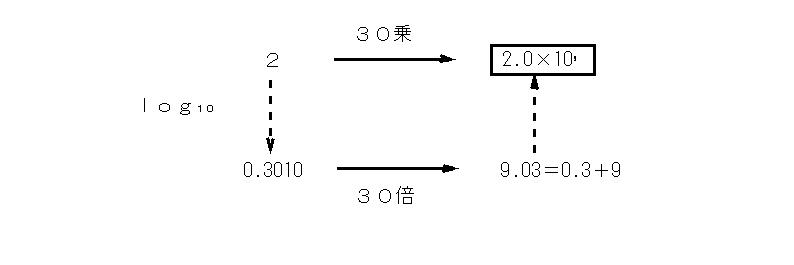
Ⅱの解答
何題か練習していく内に生徒たちは、すべての類題が計算できるようになり、また、対数のイメージがつかめるようになるのである。前任校の生徒たちでもほぼ100%の生徒たちがこの問題を解けるようになった。
まとめとして次のようにいう。
「数式操作や記号操作の背景には、というより数式操作や記号操作の内には意味やイメージが必ずある。今回例14の問題を通して、その点がわかったと思う。イメージや意味がつかめれば、君たちにとって数学は身近なものになるはずだ。記号や式には、イメージが潜在している。潜在しているイメージを掴んでやることが大切であり、真の理解なのである。常にどんなイメージが潜在しているのか考える習慣をぜひともつけてほしい。」
以上が、まとめまでの展開例である。おそらく2回の授業によって、対数への興味(そして数学自体に対する興味も)は以前より深まっているはずである。この2回の授業のなかには、割り箸で計算尺を作る作業学習が取り入れられているし、また、模式図を使って、イメージが喚起できるようになっている。普段より右脳はかなり刺激され、使われたはずである。
最後には問題演習の時間をとり、問題を解かせる。もちろんここでは、記号操作によって解かせるのである。前回2回の授業で、痛切な印象を持っているので、式に潜んでいるイメージが何であるか考えるであろう。イメージは、生徒たちの力では、必ずしもつかめるものではない。だが、努力するだけでも彼らの右脳は鍛えられるのである。右脳が鍛えられれば、少しずつイメージがつかめるようになるに違いないのである。もちろん、イメージがつかめないでへこたれそうになる場面では指導者の援助が必要である。