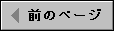第1節 速さ
「時間=道のり÷速さ」という公式ほどばかげた公式はない。誰が遅刻しそうになっているときに、時間は道のり÷速さだから時間を短縮するためには、歩みの速度を上げなければならない、と考えるだろうか。このままでは遅刻だと思えば、反射的に走り出すであろう。論理など介在する余地なく直観的に結論を出すのである。現在の算数教育は、この比喩のばかげた迂路を児童に強いているのである。直観算数では、日常における思考の働きと同じ発想をしよう、と提唱するのである。それは生活臭のある算数だ。
速さの単元で必要な事柄は、「速さは単位時間あたりの道のりである。」の1つである。これ以外何も必要でないし、これ以外何も教えるべきではない。速さの単元に出てくるすべての問題は、この1つさえ知っていればすべて解くことができるのである。「速さ=道のり÷時間、道のり=速さ×時間、時間=道のり÷速さ」などの公式は、一切必要としない。
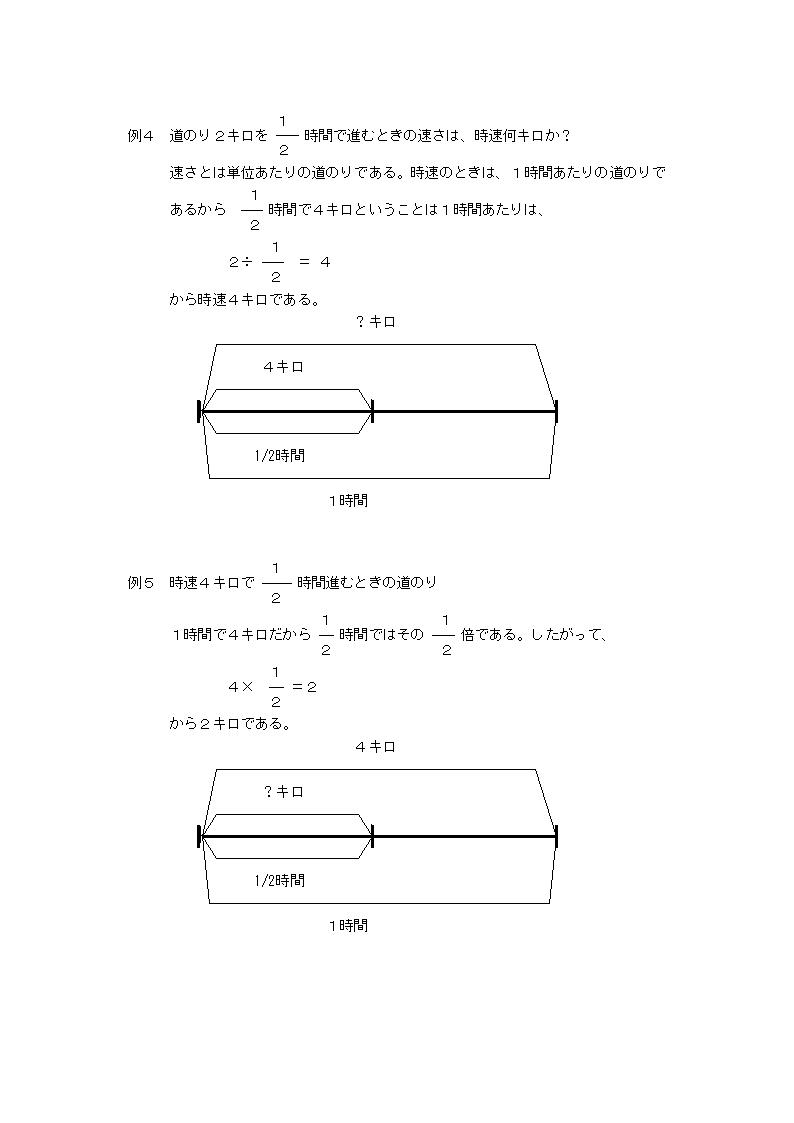
例1 道のり8キロを2時間で進むときの速さは、時速何キロか?
速さとは単位あたりの道のりである。時速のときは、1時間あたりの道のりであるから、2時間で8キロということは1時間あたりは、
8÷2=4
から時速4キロである。
この問題を考える際に大事なのは、下の図を書くことである。
線分図を必ず書くことが直観を育てるために絶対に必要である。
例2 時速4キロで2時間進むときの道のり
1時間で4キロだから2時間ではその2倍である。したがって、
4×2=8
から8キロである。

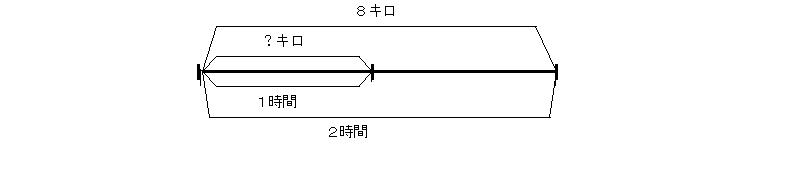
例3 8キロの道のりを時速4キロで進むときの時間
1時間で4キロ進むから8キロ進むのにかかる時間は8のなかに4がいくつ入っていればいいかを考えればいいから
8÷4=2
の計算から2時間である。
「以上の計算にどうして公式がいるだろうか。うまく指導すれば、直観的に答えられるようになるはずだ。」といいたいところであるが、実際上は分数や小数が出てくると、児童は混乱してしまう。以下の例だ。