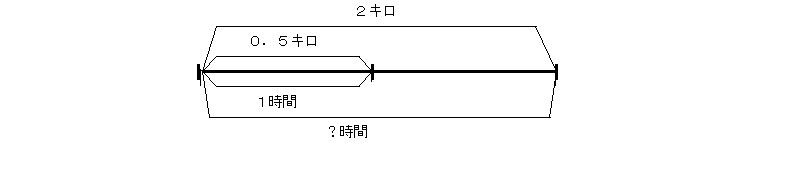
1時間で0.5キロ進むから2キロ進むのにかかる時間は2のなかに0.5がいくつはいっていればいいかを考えればいいから
2÷0.5=4
の計算から4時間である。
例の4,5,6は例の1,2,3とそれぞれ同じであり、何も変わるところはない。ところが左脳化している児童には、両者の同一性はまったくわからない。分数が入ってきた瞬間に多くの児童は拒絶反応を示してしまう。彼らには類推的直観は働かない。ここの把握は、おそらくフッサールがいうのところの本質直観とでも言うべきものである。本質直観とは,1つの類例から、想像的変容によって本質すなわち普遍を把握してしまう直観である。
理論的話は別にしても、なぜ彼らは本質的はまったく同じである例1と例4を別のものと考える、または捉えてしまうのだろか。それは彼らの分数や小数の把握が不十分だからである。彼らの分数理解は、直観のレベルに達していないのである。言い換えれば、分数や小数を感覚的に把握していないのである。分数や小数が、血となり肉となっていないのだ。ここでも彼らの理解は、形式のレベルにとどまっている。1/2という場合、お饅頭の半分というように、具象的なものがイメージされていなければならない。ところが、先生たちは導入の段階でこそお饅頭やミカンなどを利用するであろうが、分数の途中の単元から機械的な指導に終始してしまっているというのが、実態なのではないだろうか。分数の単元においてはもちろんのこと、いかなる段階でも(ということは分数の指導が終わった後でもということである。)指導者は、ミカンやお饅頭の比喩を入れて話してやるべきなのである。1/2という形式(入れ物)のなかに半分のお饅頭や半分のミカンいうイメージが、自由に出入りできるのでなければならない。私は、形式のなかに内容が入ってくることを、フッサールの用語を借りて直観充当ないしは意味充当と呼ぶ。算数教育及び数学教育のなかで決定的に不足しているものは、この直観充当すなわち意味充当である。私は直観充当されて、血となり肉となった算数及び数学を提唱しているのである。直観充当意味充当は、それによって血となり肉となるのだから受肉と呼んでもいい。私が直観算数や直観数学という場合、それは受肉された算数や数学を意味している。イエス・キリストは受肉されて人間になったのだから、算数や数学の人間化と言ってもいい。
またまた話が理論的になってしまったので、話を元に戻そう。例1と例4の2つの式
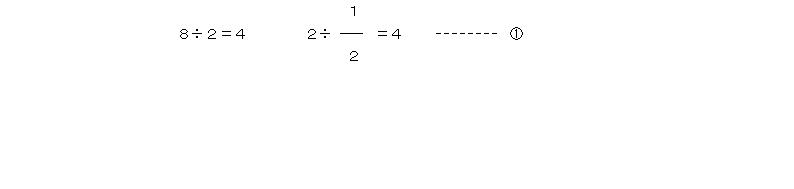
を比べたとき、確かに後半のわり算の方がわかりにくいことは事実である。30年も前のことなので記憶は定かではないが、私はおそらく次のように処理していたと思う。
2×2=4
後半の2は、1時間は1/2時間の何倍かを示している。①の式にこだわることはない。問題を解くのにはどんな方法でもいいのである。いろいろ発想ができる方が、柔軟な頭脳を鍛えるのにいいのである。1つの方法に限定しない点が、右脳数学・右脳算数の眼目の1つなのである。公式による指導は、方法を限定してしまう。
公式による指導がなぜ問題なのか。これについては後で、1つの章をも設けて詳論する予定になっているが、簡単に述べると「公式は本質を隠蔽し遮断する」すると言うことである。つまりなぜわり算になるのか、かけ算になるのかという本質的な問いを遮断してしまい、思考を停止させてしまう。1回1回それぞれの問題場面において、かけ算になるかわり算になるのかを本質から考えることが大切なのに、考えなくて済む方法が公式による方法なのである。考えなくても済むからこそ、児童は歓迎するのである。だが、これは右脳の遮断であり、右脳を休眠させる行為である。これでは右脳は鍛えられない。
先の①の式に話を戻そう。①の左の式はわかりやすい。1時間あたりの量を出すには、2分割してやればいいのだから。だが、例4において1時間あたりの量を出すのに、なぜわり算になるのかはわかりにくい。単位量あたりの量を出すには、わり算になると、いくつかの例を示して一般化してしまってもよいが、これは一種の公式化である。だが「速さ=道のり÷時間」に比べれば、ずっと具象的である。なぜなら、線分図を媒介にして一般化しているからである。そして、より普遍化している。速さだけでなく、割合やその他の単元にも適用することのできる、考え方であるからである。だから、右脳と左脳のもっともうまい協同例といえないことはない。しかし、あくまで直観にこだわってみよう。
場面によっては考えにくい数字の場合、私は考えやすい数字なおして考えていた。つまり、例4を例1のような問題に変換して式を出していたわけだ。ここには類推的直観が作用している。フッサールがいうところの想像的変容による本質直観に相当するものであると思われる。これは私の1つの解決方法であったが、それ以外にもいろいろ思考していたような気がする。実際上の計算は先に書いたように、
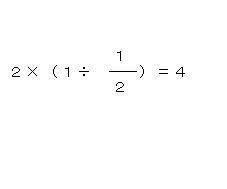
と計算していたと思う。つまり、1時間のなかには1/2時間が何個はいっているかを考え、2個入っているので2倍すると思考していたのである。ここには公式の入る余地はどこにもなかった。
次の例5についてみてみよう。時速4キロで1/2時間進む場合の道のりを求める問題であった。
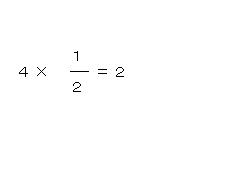
ここでも上の式は、公式を使わない限り多くの児童から出てこない。これは児童たちに1/2倍という概念がないためだ。これは次の節で扱う割合の直観的理解ができていないというという問題である。割合を理解することが、実は非常に重要なのである。例6を理解するためにはやはり割合の理解が大切である。