算数の中でもっとも重要でありながら、児童にとってもっとも苦手な単元は割合である。割合を理解するか理解しないかが、算数を好きにし得意にするか、嫌いにし苦手にしてしまうか、の分かれ目と言ってもいい。割合を理解が、速さなど他の単元の理解に決定的な影響を与える。割合のなかに算数の秘密の半分が入っているといっても過言ではない。
割合の定義は、「割合とは比べられる量がもとにする量の何倍であるかを示す量である」、というものである。この定義に割合の単元で学ぶすべてが入っている。私が意味からの算数教育という場合、この定義以外何も教えるな!ということを意味している。つまり割合のすべての問題は、この定義に戻って考えよ、ということなのである。「割合=比べられる量÷もとにする量」、「比べられる量=もとにする量×割合」、「もとにする量=比べられる量÷割合」の3つの公式は一切使う必要がない。使う必要がないどころか、公式は有害ですらある。「公式は本質を隠蔽する。」
例1 8cmの4cmに対する割合を求めよ。
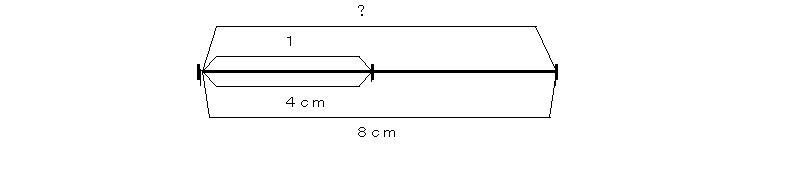
割合は、比べられる量がもとにする量の何倍であるかを示す数字である。したがって、この問題は8cmが4cmの何倍であるかと聞いている。つまり8のなかには4がいくつ入っているかと聞いているのである。だから、
8÷4=2
の計算から割合は2である。
線分図では、上に割合下に実際の数や量がかかれている。上下の役割を決めてしまうと、一種の公式主義になってしまうが、指導のはじめの内ははっきり決めておいた方がいい。割合が理解できなくなるなる大きな原因の一つが、実際の量と割合の混乱にある。実際の量は、単位がある量であり、割合は単位のない量である。したがって、割合とはかなり抽象的な概念である。だが、鍛え方では割合という概念は直観の領域へすなわち右脳の領域に入って来るのである。車の運転を習いはじめのときには、頭で坂道発信するにはサイドブレーキを引いて、エンジンを吹かせてからブレーキを下ろす、と反芻してから実際に行動しているはずである。ところが、熟練のドライバーそんなことは考えず、反射的に行っているはずである。これは最初左脳の領域にあったものが、右脳の領域に移ったことを意味している。つまり論理から直観に移行したのである。先に直観は、論理を支える柱であるといったが、逆に論理の反復が直観を形成していく場合もあるのである。「常に形式は内容的であり、常に内容は形式的である。」(ヘーゲル「小論理学」など) 割合についても、訓練を続ける内に右脳の領域へ、つまり直観の領域に移っていけるのである。あくまで時間をかければということである。ここに時間をかけないで、性急な結果を求めることに左脳主義に陥る原因がある。分数や小数についても感覚的な理解がないのは、訓練不足に起因する。
例2 4cmに対するあるものの割合が2である。あるものはいくつか。
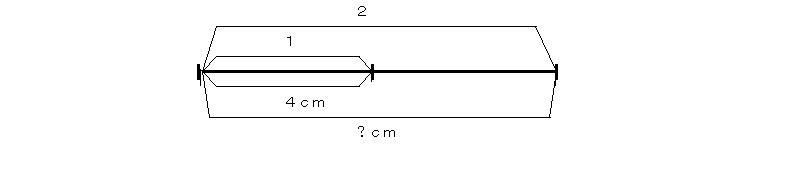
あるものは4cmの2倍だといっているのだから
4×2=8
の計算から8cmである。
例3 あるものに対する8cmの割合が2である。あるものを求めよ。
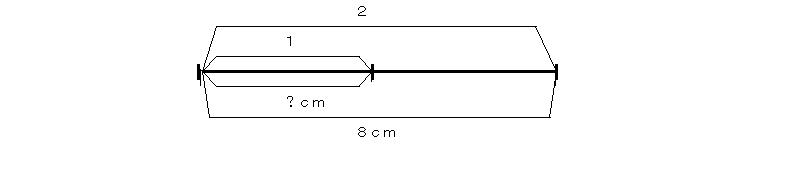
割合2で8cmだから割合1に対してはその半分で(あるいは2倍したら8cmになるのだから)
8÷2=4 ないしは 8×1/2=4
の計算から4cmである。
以上例1から例3までは、公式がいらないということは納得してもらえると思う。ところが問題は、速さのときと同じで、数値が分数や小数になるときである。つまり以下の例である。ここでも先の速さのときと同じ拒絶反応に出会うことになる。
例4 4cmの8cmに対する割合を求めよ。
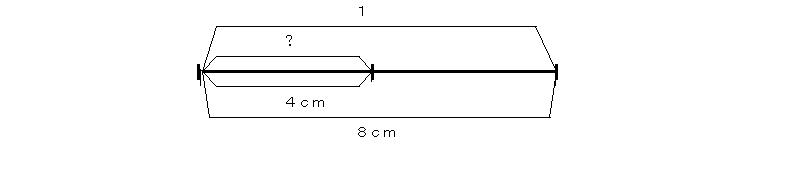
割合は、比べられる量がもとにする量の何倍であるかを示す数字である。したがって、この問題は4cmが8cmの何倍であるかと聞いている。つまり8のなかには4が いくつ入っているかと聞いているのである。だから、
4÷8=4/8=1/2
の計算から割合は1/2である。
例5 8cmに対するあるものの割合が1/2である。あるものはいくつか。
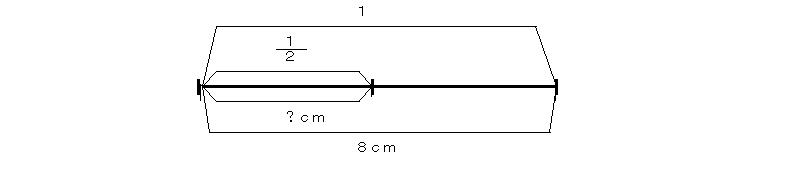
あるものは8cmの1/2倍だといっているのだから
8× 1/2 =4
の計算から4cmである。
例6 あるものに対する4cmの割合が1/2である。あるものを求めよ。
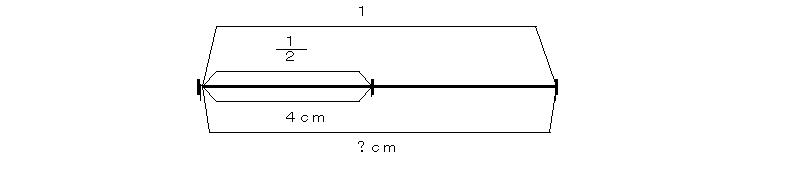
割合1/2で4cmだから割合1に対してはその2倍で(あるいは2倍したら8cmに
なるのだから)
4×2=8 ないしは 4÷1/2=8
の計算から4cmである。速さの例4のときと同じで、後半のわり算は確かにわかりにくいで、単位あたりの量はわり算で出すという点だけ、公式化してもよい。
例4から例6までの拒絶反応については、速さのときと同じである。充分な訓練によって、分数が血となり肉となっていないための反応である。だから分数指導も、もちろん改革されなければならないが、しかし割合や速さの単元で決して公式を使用しないで、忍耐強く指導を続けるならば、分数に対するアレルギーもなくなっていくはずである。1つ1つ丁寧にねばり強く説明して、児童を訓練させていけば必ず理解できるはずである。先にあげた運転の例と同じで、ねばり強い指導によって直観の領域に移行できるはずである。絶対に性急な指導しなければの話である。