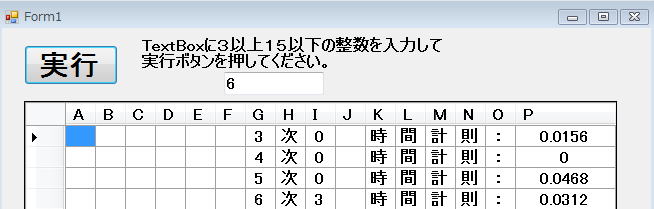
label2のテキストは消してありますが、赤囲いの中にlabe2が挿入してあります。
今まで入れてきませんでしたが、TextBoxに範囲外の整数が入力されている場合
『TextBoxには3以上11以下の整数を入力し再度実行ボタンを押して下さい。』と表示させるために今回入れました。
(今までのソフトも同様に是非改良して下さい。)
それに対応するのが下のソースのピンクです。尚、青色の部分は乱数最適実験によってsrand()内の数字を決めました。
乱数最適実験プログラムはこの後示します。
そして、赤こそが驚異の結果をもたらせてくれた各3行です。茶色は、これに伴って変更した箇所です。
また、syokika();は処理内容が多くなったので関数として独立させました。
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
label2->Text=L"";
DateTime^ hj=DateTime::Now;
n=int::Parse(textBox1->Text);
int h=1;
if(n<3 || n>=12){
label2->Text=L"TextBoxには3以上11以下の整数\r\nを入力し再度実行ボタンを\r\n押して下さい。";
h=0;
}
if(h==1){
s=0;
if(n%2==1)g1(n);
if(n%2==0)g2(n);
syokika();
if(n==3 || n==4)srand(0);
if(n==5)srand(3);
if(n==6)srand(17);
if(n==7)srand(95);
if(n==8)srand(1845);
if(n==9)srand(4860);
if(n==10)srand(9877);
f1(0);
array<String^>^ w=gcnew array<String^>(16);
int i;
w[10]=n.ToString();w[11]=L"次";w[12]=L"魔";w[13]=L"方";w[14]=L"陣";w[15]=L"の場合";
for(i=0;i<9;i++)w[i]=L"";
dataGridView1->Rows->Add(w);
DateTime^ ow=DateTime::Now;
TimeSpan sa=ow->Subtract(*hj);
w[10]=L"時";w[11]=L"間";w[12]=L"計";w[13]=L"則";w[14]=L":";w[15]=(sa.TotalSeconds).ToString();
for(i=0;i<10;i++)w[i]=L"";
dataGridView1->Rows->Add(w);
}
}
void syokika(){
int i,j;
for(i=0;i<n;i++){
cn1[i]=0;cn2[i]=0;
for(j=0;j<n;j++){
p[i][j]=0;
}
}
}
・
・
・
void f1(int g){
kkk=(kk+i)%n;
a1[y[g]][x[g]]=kkk;
h=1;
for(i=0;i<n;i++){
・
・
・
cn1[kkk]++;
if(cn1[kkk]>n)h=0;
if(h==1){
if(g==n-1){
wa=0;
for(j=0;j<n;j++){
wa+=a1[j][j];
if(wa!=n*(n-1)/2)h=0;
}
}
}
・
・
・
if(h==1){
if(g<n*n-1){
f1(g+1);
}
else{
f2(0);
if(s==1)return;
}
}
cn1[kkk]--;
}
}
void f2(int g){
・
・
・
for(i=0;i<n;i++){
・
・
・
h=1;
cn2[kkk]++;
if(cn2[kkk]>n)h=0;
hh=0;
if(h==1){
if(p[yy][xx]==0){
p[yy][xx]=1;
hh=1;
}
else{
h=0;
}
・
・
・
if(h==1){
if(g<n*n-1){
f2(g+1);
}
else{
for(j=0;j<n;j++){
for(k=0;k<n;k++){
w[k]=(n*a1[j][k]+a2[j][k]+1).ToString();
}
dataGridView1->Rows->Add(w);
}
for(j=0;j<16;j++)w[j]=L"";
dataGridView1->Rows->Add(w);
s++;
if(s==1)return;
}
}
if(hh==1)p[yy][xx]=0;
cn2[kkk]--;
}
}
ダウンロード用ファイルForm3.h(自分の該当フォルダに貼り付けるときは、名前をForm1.hに変更してから貼り付けてください。)
乱数最適実験ですが、そのソースは上のForm3.hファイルを次のように変更して作りました。
DateTime^ hj;
DateTime^ ow;
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
n=int::Parse(textBox1->Text);
s=0;
if(n%2==1)g1(n);
if(n%2==0)g2(n);
for(sk=0;sk<20000;sk++){
hj=DateTime::Now;
syokika();
int i;
srand(sk);
f1(0);
array<String^>^ w=gcnew array<String^>(16);
ow=DateTime::Now;
TimeSpan sa=ow->Subtract(*hj);
if(s>0){
w[6]=n.ToString();w[7]="次";w[8]=sk.ToString();w[9]=L"";w[10]=L"時";w[11]=L"間";w[12]=L"計";w[13]=L"則";w[14]=L":"; w[15]=(sa.TotalSeconds).ToString();
for(i=0;i<6;i++)w[i]=L"";
dataGridView1->Rows->Add(w);
break;
}
s=0;
}
}
void f1(int g){
if(s==1)return;
ow=DateTime::Now;
TimeSpan sa=ow->Subtract(*hj);
if(sa.TotalSeconds>0.05)return;