TextBoxに例えば6を入れて実行ボタンを押すと、
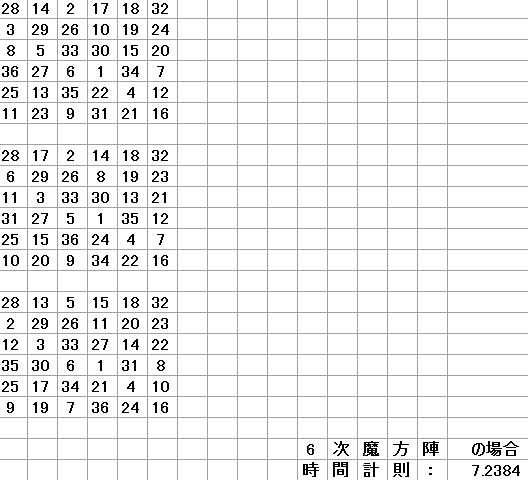
100個で7.2384秒ですから、1個あたり0.07284秒です。
今までのソフトでは歯が立たなかった6次魔方陣が1個あたり平均で0.1秒もかからずにできてしまいます。
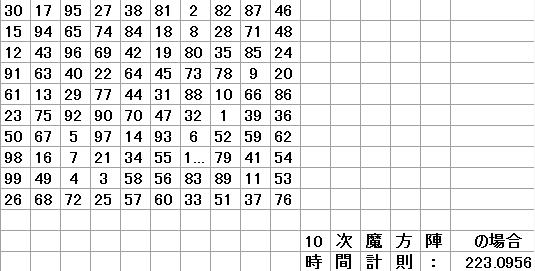
総計約223秒で、1個あたりの平均は約2.23秒です。
驚異的スピードです。
さて、10次魔方陣を例にとり解説していきましょう。
第20講 一般種法による魔方陣ソフトの高速化
第9話 模範解答例解説
前回のif(s==1)return; をif(s==100)return; と変更すれば100個作成させることができます。
TextBoxに例えば6を入れて実行ボタンを押すと、

100個で7.2384秒ですから、1個あたり0.07284秒です。
今までのソフトでは歯が立たなかった6次魔方陣が1個あたり平均で0.1秒もかからずにできてしまいます。

総計約223秒で、1個あたりの平均は約2.23秒です。
驚異的スピードです。
さて、10次魔方陣を例にとり解説していきましょう。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | 0 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 10 |
| 1 | 28 | 1 | 36 | 37 | 38 | 39 | 40 | 41 | 11 | 42 |
| 2 | 29 | 43 | 2 | 50 | 51 | 52 | 53 | 12 | 54 | 55 |
| 3 | 30 | 44 | 56 | 3 | 62 | 63 | 13 | 64 | 65 | 66 |
| 4 | 31 | 45 | 57 | 67 | 4 | 14 | 72 | 73 | 74 | 75 |
| 5 | 32 | 46 | 58 | 68 | 15 | 5 | 80 | 81 | 82 | 83 |
| 6 | 33 | 47 | 59 | 16 | 76 | 84 | 6 | 88 | 89 | 90 |
| 7 | 34 | 48 | 17 | 69 | 77 | 85 | 91 | 7 | 94 | 95 |
| 8 | 35 | 18 | 60 | 70 | 78 | 86 | 92 | 96 | 8 | 98 |
| 9 | 19 | 49 | 61 | 71 | 79 | 87 | 93 | 97 | 99 | 9 |
f1やf2におけるfor文中の
if(cn1[kkk]>n)h=0;はすべてのセル(升)で実行されますが、
他のif文が実行されるのは下記の、水色以外のセルにおいてです。
| y | ||||||||||||
| ↓ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ← | x |
| 0 | 0 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 10 | ||
| 1 | 28 | 1 | 36 | 37 | 38 | 39 | 40 | 41 | 11 | 42 | ||
| 2 | 29 | 43 | 2 | 50 | 51 | 52 | 53 | 12 | 54 | 55 | ||
| 3 | 30 | 44 | 56 | 3 | 62 | 63 | 13 | 64 | 65 | 66 | ||
| 4 | 31 | 45 | 57 | 67 | 4 | 14 | 72 | 73 | 74 | 75 | ||
| 5 | 32 | 46 | 58 | 68 | 15 | 5 | 80 | 81 | 82 | 83 | ||
| 6 | 33 | 47 | 59 | 16 | 76 | 84 | 6 | 88 | 89 | 90 | ||
| 7 | 34 | 48 | 17 | 69 | 77 | 85 | 91 | 7 | 94 | 95 | ||
| 8 | 35 | 18 | 60 | 70 | 78 | 86 | 92 | 96 | 8 | 98 | ||
| 9 | 19 | 49 | 61 | 71 | 79 | 87 | 93 | 97 | 99 | 9 |
ソースとセル色を対応させておくと
if(h==1){
if(g==n-1){
wa=0;
for(j=0;j<n;j++){
wa+=a1[j][j];
}
if(wa!=n*(n-1)/2)h=0;
}
}
if(h==1){
if(y[g]==n-1 && x[g]==0){
wa=0;
for(j=0;j<n;j++){
wa+=a1[n-1-j][j];
}
if(wa!=n*(n-1)/2)h=0;
}
}
if(h==1){
if(y[g]==0 && x[g]==n-2){
wa=0;
for(j=0;j<n;j++){
wa+=a1[y[g]][j];
}
if(wa!=n*(n-1)/2)h=0;
}
}
if(h==1){
if(y[g]==n-2 && x[g]==0){
wa=0;
for(j=0;j<n;j++){
wa+=a1[j][x[g]];
}
if(wa!=n*(n-1)/2)h=0;
}
}
if(h==1){
if(y[g]>0 && y[g]<n-1 && x[g]==n-1){
wa=0;
for(j=0;j<n;j++){
wa+=a1[y[g]][j];
}
if(wa!=n*(n-1)/2)h=0;
}
}
if(h==1){
if(x[g]>0 && x[g]<n-1 && y[g]==n-1){
wa=0;
for(j=0;j<n;j++){
wa+=a1[j][x[g]];
}
if(wa!=n*(n-1)/2)h=0;
}
}
となります。
それぞれの水色以外の色のセルに達したとき何をしているかというと、
対角線や行、列などを合計させ合計がn*(n−1)/2に等しくないときはhを0にし、
等しいときは何もしない、すなわちhは1のままにしておくようにしています。
| y | ||||||||||||
| ↓ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ← | x |
| 0 | 0 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 10 | ||
| 1 | 28 | 1 | 36 | 37 | 38 | 39 | 40 | 41 | 11 | 42 | ||
| 2 | 29 | 43 | 2 | 50 | 51 | 52 | 53 | 12 | 54 | 55 | ||
| 3 | 30 | 44 | 56 | 3 | 62 | 63 | 13 | 64 | 65 | 66 | ||
| 4 | 31 | 45 | 57 | 67 | 4 | 14 | 72 | 73 | 74 | 75 | ||
| 5 | 32 | 46 | 58 | 68 | 15 | 5 | 80 | 81 | 82 | 83 | ||
| 6 | 33 | 47 | 59 | 16 | 76 | 84 | 6 | 88 | 89 | 90 | ||
| 7 | 34 | 48 | 17 | 69 | 77 | 85 | 91 | 7 | 94 | 95 | ||
| 8 | 35 | 18 | 60 | 70 | 78 | 86 | 92 | 96 | 8 | 98 | ||
| 9 | 19 | 49 | 61 | 71 | 79 | 87 | 93 | 97 | 99 | 9 |
| y | ||||||||||||
| ↓ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ← | x |
| 0 | 0 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 10 | ||
| 1 | 28 | 1 | 36 | 37 | 38 | 39 | 40 | 41 | 11 | 42 | ||
| 2 | 29 | 43 | 2 | 50 | 51 | 52 | 53 | 12 | 54 | 55 | ||
| 3 | 30 | 44 | 56 | 3 | 62 | 63 | 13 | 64 | 65 | 66 | ||
| 4 | 31 | 45 | 57 | 67 | 4 | 14 | 72 | 73 | 74 | 75 | ||
| 5 | 32 | 46 | 58 | 68 | 15 | 5 | 80 | 81 | 82 | 83 | ||
| 6 | 33 | 47 | 59 | 16 | 76 | 84 | 6 | 88 | 89 | 90 | ||
| 7 | 34 | 48 | 17 | 69 | 77 | 85 | 91 | 7 | 94 | 95 | ||
| 8 | 35 | 18 | 60 | 70 | 78 | 86 | 92 | 96 | 8 | 98 | ||
| 9 | 19 | 49 | 61 | 71 | 79 | 87 | 93 | 97 | 99 | 9 |
| y | ||||||||||||
| ↓ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ← | x |
| 0 | 0 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 10 | ||
| 1 | 28 | 1 | 36 | 37 | 38 | 39 | 40 | 41 | 11 | 42 | ||
| 2 | 29 | 43 | 2 | 50 | 51 | 52 | 53 | 12 | 54 | 55 | ||
| 3 | 30 | 44 | 56 | 3 | 62 | 63 | 13 | 64 | 65 | 66 | ||
| 4 | 31 | 45 | 57 | 67 | 4 | 14 | 72 | 73 | 74 | 75 | ||
| 5 | 32 | 46 | 58 | 68 | 15 | 5 | 80 | 81 | 82 | 83 | ||
| 6 | 33 | 47 | 59 | 16 | 76 | 84 | 6 | 88 | 89 | 90 | ||
| 7 | 34 | 48 | 17 | 69 | 77 | 85 | 91 | 7 | 94 | 95 | ||
| 8 | 35 | 18 | 60 | 70 | 78 | 86 | 92 | 96 | 8 | 98 | ||
| 9 | 19 | 49 | 61 | 71 | 79 | 87 | 93 | 97 | 99 | 9 |
| y | ||||||||||||
| ↓ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ← | x |
| 0 | 0 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 10 | ||
| 1 | 28 | 1 | 36 | 37 | 38 | 39 | 40 | 41 | 11 | 42 | ||
| 2 | 29 | 43 | 2 | 50 | 51 | 52 | 53 | 12 | 54 | 55 | ||
| 3 | 30 | 44 | 56 | 3 | 62 | 63 | 13 | 64 | 65 | 66 | ||
| 4 | 31 | 45 | 57 | 67 | 4 | 14 | 72 | 73 | 74 | 75 | ||
| 5 | 32 | 46 | 58 | 68 | 15 | 5 | 80 | 81 | 82 | 83 | ||
| 6 | 33 | 47 | 59 | 16 | 76 | 84 | 6 | 88 | 89 | 90 | ||
| 7 | 34 | 48 | 17 | 69 | 77 | 85 | 91 | 7 | 94 | 95 | ||
| 8 | 35 | 18 | 60 | 70 | 78 | 86 | 92 | 96 | 8 | 98 | ||
| 9 | 19 | 49 | 61 | 71 | 79 | 87 | 93 | 97 | 99 | 9 |
| y | ||||||||||||
| ↓ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ← | x |
| 0 | 0 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 10 | ||
| 1 | 28 | 1 | 36 | 37 | 38 | 39 | 40 | 41 | 11 | 42 | ||
| 2 | 29 | 43 | 2 | 50 | 51 | 52 | 53 | 12 | 54 | 55 | ||
| 3 | 30 | 44 | 56 | 3 | 62 | 63 | 13 | 64 | 65 | 66 | ||
| 4 | 31 | 45 | 57 | 67 | 4 | 14 | 72 | 73 | 74 | 75 | ||
| 5 | 32 | 46 | 58 | 68 | 15 | 5 | 80 | 81 | 82 | 83 | ||
| 6 | 33 | 47 | 59 | 16 | 76 | 84 | 6 | 88 | 89 | 90 | ||
| 7 | 34 | 48 | 17 | 69 | 77 | 85 | 91 | 7 | 94 | 95 | ||
| 8 | 35 | 18 | 60 | 70 | 78 | 86 | 92 | 96 | 8 | 98 | ||
| 9 | 19 | 49 | 61 | 71 | 79 | 87 | 93 | 97 | 99 | 9 |
| y | ||||||||||||
| ↓ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ← | x |
| 0 | 0 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 10 | ||
| 1 | 28 | 1 | 36 | 37 | 38 | 39 | 40 | 41 | 11 | 42 | ||
| 2 | 29 | 43 | 2 | 50 | 51 | 52 | 53 | 12 | 54 | 55 | ||
| 3 | 30 | 44 | 56 | 3 | 62 | 63 | 13 | 64 | 65 | 66 | ||
| 4 | 31 | 45 | 57 | 67 | 4 | 14 | 72 | 73 | 74 | 75 | ||
| 5 | 32 | 46 | 58 | 68 | 15 | 5 | 80 | 81 | 82 | 83 | ||
| 6 | 33 | 47 | 59 | 16 | 76 | 84 | 6 | 88 | 89 | 90 | ||
| 7 | 34 | 48 | 17 | 69 | 77 | 85 | 91 | 7 | 94 | 95 | ||
| 8 | 35 | 18 | 60 | 70 | 78 | 86 | 92 | 96 | 8 | 98 | ||
| 9 | 19 | 49 | 61 | 71 | 79 | 87 | 93 | 97 | 99 | 9 |
最後の2つは例。
1行から8行まで、
1列から8列まで、
すべて同様である。
if(h==1){
if(y[g]==0 && x[g]==n-2){
wa=0;
for(j=0;j<n;j++){
wa+=a1[y[g]][j];
}
if(wa!=n*(n-1)/2)h=0;
}
}
if(h==1){
if(y[g]==n-2 && x[g]==0){
wa=0;
for(j=0;j<n;j++){
wa+=a1[j][x[g]];
}
if(wa!=n*(n-1)/2)h=0;
}
}
の2つは必要です。それは、gの動きを見れば分かります。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0 | 0 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 10 |
| 1 | 28 | 1 | 36 | 37 | 38 | 39 | 40 | 41 | 11 | 42 |
| 2 | 29 | 43 | 2 | 50 | 51 | 52 | 53 | 12 | 54 | 55 |
| 3 | 30 | 44 | 56 | 3 | 62 | 63 | 13 | 64 | 65 | 66 |
| 4 | 31 | 45 | 57 | 67 | 4 | 14 | 72 | 73 | 74 | 75 |
| 5 | 32 | 46 | 58 | 68 | 15 | 5 | 80 | 81 | 82 | 83 |
| 6 | 33 | 47 | 59 | 16 | 76 | 84 | 6 | 88 | 89 | 90 |
| 7 | 34 | 48 | 17 | 69 | 77 | 85 | 91 | 7 | 94 | 95 |
| 8 | 35 | 18 | 60 | 70 | 78 | 86 | 92 | 96 | 8 | 98 |
| 9 | 19 | 49 | 61 | 71 | 79 | 87 | 93 | 97 | 99 | 9 |
g=27のとき、すでにg=10には数字が入っています。ですから、この段階で
| y | ||||||||||||
| ↓ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ← | x |
| 0 | 0 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 10 | ||
| 1 | 28 | 1 | 36 | 37 | 38 | 39 | 40 | 41 | 11 | 42 | ||
| 2 | 29 | 43 | 2 | 50 | 51 | 52 | 53 | 12 | 54 | 55 | ||
| 3 | 30 | 44 | 56 | 3 | 62 | 63 | 13 | 64 | 65 | 66 | ||
| 4 | 31 | 45 | 57 | 67 | 4 | 14 | 72 | 73 | 74 | 75 | ||
| 5 | 32 | 46 | 58 | 68 | 15 | 5 | 80 | 81 | 82 | 83 | ||
| 6 | 33 | 47 | 59 | 16 | 76 | 84 | 6 | 88 | 89 | 90 | ||
| 7 | 34 | 48 | 17 | 69 | 77 | 85 | 91 | 7 | 94 | 95 | ||
| 8 | 35 | 18 | 60 | 70 | 78 | 86 | 92 | 96 | 8 | 98 | ||
| 9 | 19 | 49 | 61 | 71 | 79 | 87 | 93 | 97 | 99 | 9 |
行の和を求めておく必要があります。
g=35のときも、
すでにg=19に数字が埋められています。やはり、この段階で
| y | ||||||||||||
| ↓ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ← | x |
| 0 | 0 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 10 | ||
| 1 | 28 | 1 | 36 | 37 | 38 | 39 | 40 | 41 | 11 | 42 | ||
| 2 | 29 | 43 | 2 | 50 | 51 | 52 | 53 | 12 | 54 | 55 | ||
| 3 | 30 | 44 | 56 | 3 | 62 | 63 | 13 | 64 | 65 | 66 | ||
| 4 | 31 | 45 | 57 | 67 | 4 | 14 | 72 | 73 | 74 | 75 | ||
| 5 | 32 | 46 | 58 | 68 | 15 | 5 | 80 | 81 | 82 | 83 | ||
| 6 | 33 | 47 | 59 | 16 | 76 | 84 | 6 | 88 | 89 | 90 | ||
| 7 | 34 | 48 | 17 | 69 | 77 | 85 | 91 | 7 | 94 | 95 | ||
| 8 | 35 | 18 | 60 | 70 | 78 | 86 | 92 | 96 | 8 | 98 | ||
| 9 | 19 | 49 | 61 | 71 | 79 | 87 | 93 | 97 | 99 | 9 |
列の合計を調べなければなりません。
これで第20講は終わりにします。
大変、難解な講義になってしまいました。
難解な講義を読んで頂いて、ありがとうございます。
ここまで読んできた皆さんは、もう初心者の域を脱しています。
すでに、中級に達したと言っていいでしょう。
講義の大体の予定を話しておきますと、
第21講では、末項確定法(今まで残確定法と呼んでいましたが、名称を末項確定法に変更します。)
による魔方陣ソフトのさらなる高速化に挑戦します。
第22講では、素数探索を題材にマルチスレッドプログラミングに挑みます。
CPUを4つ積んでいるパソコンでは、今回挑戦した一般種法による魔方陣作成ソフトをランさせているとき、
CPU使用率は、25%程度に過ぎません。
つまり、4つ積んでいるのに、実質1個分しか働かせていないことになります。
3つは遊んでいるのに等しいわけです。
これからは8CPUが普通になると言われています。
そうすると、現在のままのソフトならCPU使用率は12.5%となり、
8つの内のCPUの内7つのCPUを遊ばせることになってしまいます。
8CPUなら、8つとも働かせるのがマルチスレッドプログラミングです。
マルチスレッド対応プログラムなら、CPU使用率は100%にもっていくことができます。
つまり、8CPUパソコンならマルチスレッド化すれば8倍の速度を実現できると言うことです。
第23講では、マルチスレッドによる第21講の末項確定法のさらなる高速化を図ります。
第24講では、連立方程式を解くソフトを作ります。
第20講第8話へ 第21講第1話へ

VC++講義第1部へ
vb講義へ
VB講義基礎へ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座
初心者のための世界で一番わかりやすいVisual
Basic入門基礎講座