ところが、昨日は1日かけても5次までしかできるようになりませんでした。
それで、第7話のアップを諦めて本日になってしまいました。
ですが、今日になり大きな進展=それは予想を超える驚愕天地の進展でした。
前に10次なら10分程度かかってしまうと書きましたが、
実際には10次は0.0624秒で作成できました。
昨日と今日と2日かけた戦果をご覧ください。時間の単位は秒です。
時間データはすべて私の使用パソコンによります。
使用感環境は、Intel(R)Core(TM)Quad CPU Q6600 @2.40GHz 2.40GHz

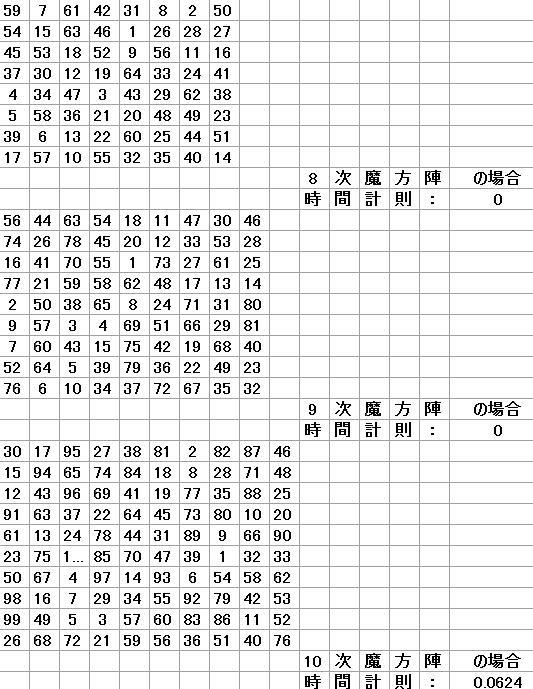
つまり、3次魔方陣から10次魔方陣まですべて1個作成するのにかかった時間は0.07秒以下です。
前の特殊種による魔方陣作成ソフトでは、9次は10時間かけても1個もできなかったのに対して、
0.001秒以下(データは0秒となっていますが0.001秒以下は計測できないと言うことでしょう。)という驚異的な時間です。
昨日1日かけてもうまくいかなかったソースを最初にご覧頂きます。
といっても、プログラミングには間違いがありません。
ですが、6次でさえ8時間コンピュータを走らせましたが、
1個もできませんでした。
かつてVBで作ったプログラミングと基本的に同じはずなのに、なぜうまくいかないのか、
1日考えてしまいました。
ソースには間違いがないと思われ、最適乱数系列を探す実験を1日中繰り返しましたが、
数秒以内に6次魔方陣などを作り出す最適乱数系列は発見することができませんでした。
(注 srand(0以上の整数);で乱数系列を指定し初期化することができます。
実験の方法については次話で紹介します。)
プログラミングが間違いないというのは、
そのプログラミングにたった6行(=f1に3行、f2に3行)付け加えただけで、
ある乱数系列の基に8時間かけてもできなかった6次魔方陣が0.001秒以下でできるようになったからです。
仮に6行加える前のソフトが8時間(実際はそれ以上でしょう)だとしても、
8×3600÷0.001=10800000(倍)=1080万(倍)を上回るほど作成速度が速くなったのです。
ソースを示しますので、どのような6行(f1に3行+f2に3行)を付け加えたのか考えてみてください。
もちろんヒントがなければ考えようがありませんから、後にヒントを書きます。
void f1(int g){
if(s==1)return;
int i,j,k,h,wa,kk,kkk,m;
kk=rand()%n;
m=n/2;
for(i=0;i<n;i++){
kkk=(kk+i)%n;
a1[y[g]][x[g]]=kkk;
h=1;
if(g==n-1){
wa=0;
for(j=0;j<n;j++){
wa+=a1[j][j];
}
if(wa!=n*(n-1)/2)h=0;
}
if(h==1){
if(y[g]==n-1 && x[g]==0){
wa=0;
for(j=0;j<n;j++){
wa+=a1[n-1-j][j];
}
if(wa!=n*(n-1)/2)h=0;
}
}
if(h==1){
if(y[g]==0 && x[g]==n-2){
wa=0;
for(j=0;j<n;j++){
wa+=a1[y[g]][j];
}
if(wa!=n*(n-1)/2)h=0;
}
}
if(h==1){
if(y[g]==n-2 && x[g]==0){
wa=0;
for(j=0;j<n;j++){
wa+=a1[j][x[g]];
}
if(wa!=n*(n-1)/2)h=0;
}
}
if(h==1){
if(y[g]>0 && y[g]<n-1 && x[g]==n-1){
wa=0;
for(j=0;j<n;j++){
wa+=a1[y[g]][j];
}
if(wa!=n*(n-1)/2)h=0;
}
}
if(h==1){
if(x[g]>0 && x[g]<n-1 && y[g]==n-1){
wa=0;
for(j=0;j<n;j++){
wa+=a1[j][x[g]];
}
if(wa!=n*(n-1)/2)h=0;
}
}
if(h==1){
if(g<n*n-1){
f1(g+1);
}
else{
f2(0);
if(s==1)return;
}
}
}
}
void f2(int g){
if(s==1)return;
int i,j,k,h,wa,kk,kkk,m,xx,yy,hh;
yy=a1[y[g]][x[g]];
array<String^>^ w=gcnew array<String^>(16);
kk=rand()%n;
m=n/2;
for(i=0;i<n;i++){
kkk=(kk+i)%n;
a2[y[g]][x[g]]=kkk;
xx=a2[y[g]][x[g]];
h=1;
hh=0;
if(p[yy][xx]==0){
p[yy][xx]=1;
hh=1;
}
else{
h=0;
}
if(h==1){
if(g==n-1){
wa=0;
for(j=0;j<n;j++){
wa+=a2[j][j];
}
if(wa!=n*(n-1)/2)h=0;
}
}
if(h==1){
if(y[g]==n-1 && x[g]==0){
wa=0;
for(j=0;j<n;j++){
wa+=a2[n-1-j][j];
}
if(wa!=n*(n-1)/2)h=0;
}
}
if(h==1){
if(y[g]==0 && x[g]==n-2){
wa=0;
for(j=0;j<n;j++){
wa+=a2[y[g]][j];
}
if(wa!=n*(n-1)/2)h=0;
}
}
if(h==1){
if(y[g]==n-2 && x[g]==0){
wa=0;
for(j=0;j<n;j++){
wa+=a2[j][x[g]];
}
if(wa!=n*(n-1)/2)h=0;
}
}
if(h==1){
if(y[g]>0 && y[g]<n-1 && x[g]==n-1){
wa=0;
for(j=0;j<n;j++){
wa+=a2[y[g]][j];
}
if(wa!=n*(n-1)/2)h=0;
}
}
if(h==1){
if(x[g]>0 && x[g]<n-1 && y[g]==n-1){
wa=0;
for(j=0;j<n;j++){
wa+=a2[j][x[g]];
}
if(wa!=n*(n-1)/2)h=0;
}
}
if(h==1){
if(g<n*n-1){
f2(g+1);
}
else{
for(j=0;j<n;j++){
for(k=0;k<n;k++){
w[k]=(n*a1[j][k]+a2[j][k]+1).ToString();
}
dataGridView1->Rows->Add(w);
}
for(j=0;j<16;j++)w[j]=L"";
dataGridView1->Rows->Add(w);
s++;
if(s==1)return;
}
}
f(hh==1)p[yy][xx]=0;
}
}
ダウンロードファイルForm2.h(該当フォルダに貼り付けるときには、Form1.hと名前を変更してください。)
