第４話 ｎ進数翻訳ソフトのコード解説
コード再掲
#pragma endregion
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
int a,n;
a=int::Parse(textBox1->Text);
n=int::Parse(textBox2->Text);
textBox3->Text=f(a,n);
}
String^ f(int a,int n){
int r;
String^ w=L"";
r=a%n;
a=a/n;
if(a>0){
w+=f(a,n);
}
else{
return(r.ToString());
}
return(w+=r);
}
};
}
このコードのポイントは、いかにして逆順を実現するかです。
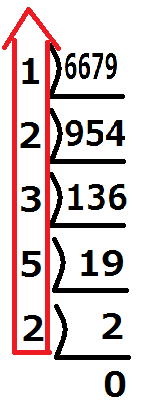（これは６６７９を７進数に翻訳しています。答えは２５３２１です。）上から番号を付けていくならそんなに悩まなくて済みます。
しかし、下から番号を付けていかなければなりません。
実は、一番自分の内なる世界まで遡及していったときに初めて、
自分の本質がわかるのです。
ユークリッド互除法において一番大切なことは、どこで終わるかです。
これが桁数を決定するからです。
内なる本質に遡及するとなると、
関数の再帰的使用が有効な手段となります。
ユークリッド互除法は、まさに関数の自己再帰にぴったりです。
自分の奥へ奥へと進み、そして自分へと再帰するからです。
私は、関数の再帰的使用を関数の自己再帰とも表現しますが、
この自己再帰には、２重の意味が込められています。
内なる自分から戻ってくるの意味と同時に、
より内なる自分への遡及自体も自己再帰であると考えているのです。
本当の自分に再び帰る、本当は知っていたけれども忘却していた自分の本質を再自覚するからです。
だから、遡及自体も自己再帰です。
逆順の実現は一番奥まで行ったとき、
すなわち一番内側の入れ子式人形にたどり着いたときに初めて、
書き込むようにすればよいのです。
それが、
if(a>0){
w+=f(a,n);
}
else{
return(r.ToString());
}
elseの部分です。
商が０になったときが、内なる旅の終点です。
このとき初めて、一番下の２が書き込まれるのです。
そして、内なる人形から自分に戻る度に
return(w+=r);
書き加えていきます。内から２番目の人形で５が書き加えられ２５となります。
以後内から３番目において３が書き加えられ２５３、
内から４番目において２が書き加えられ２５３２、
内から５番目すなわち一番外側の人形によって１が書き加えられ２５３２１となって完成するのです。
一番奥まで遡及したとき初めて書き込むことによって、逆順が実現できるのです。
では、皆さん課題です。
今回作ったソフトは、９進数までしか正確に出ません。
数字の種類が０から９までしかないからです。
１１進数以降でも正しく表示させるためには、改良が必要です。
そこで１０に相当するものをA、
１１に相当するものをB、
１２に相当するものをCなどとして表示することにしましょう。
このようにしたとき、
例えば
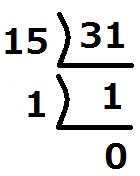３１を１６進数にしたときは１Fということになります。では皆さん、３５進数まで表示できるように変更しましょう。
３５進数までというにはアルファベット２６文字しかないからです。
数字の９種類＋アルファベット２６文字です。
もっともより大きい数字の相当するものをAaなどと表示する手もありますが、
現実には使うのはせいぜい１６進数までですから３５進数まででよいことにしましょう。
