(数独(ナンバープレイス)問題作成ソフトに挑戦する人は☆☆)
第8話 行の条件(横の条件)を加えるの解説その1
コード再掲
#pragma endregion
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
int i,j;
array<String^>^ x=gcnew array<String^>(15);
for(i=1;i<14;i++){
if(i%4==1)for(j=0;j<13;j++)x[j]=L"*";
if(i%4!=1)for(j=1;j<13;j++){
if(j%4==1)x[j]=L"*";
if(j%4!=1)x[j-1]=L"";
}
dataGridView1->Rows->Add(x);
}
}
private: System::Void button2_Click(System::Object^ sender, System::EventArgs^ e) {
int i,j;
for(i=0;i<15;i++)dataGridView1->Rows->Add();
array<String^,2>^ w=gcnew array<String^,2>(15,100);
for(i=0;i<14;i++){
for(j=0;j<14;j++){
w[i,j]=static_cast<String^>(dataGridView1[j,i]->Value);
}
}
for(i=0;i<14;i++){
for(j=0;j<14;j++){
dataGridView1[j,15+i]->Value=w[i,j];
}
}
char k1=0,k2,a[9][9];
char k,h,l;
for(i=0;i<13;i++){
if(i%4==0)k1++;
if(i%4!=0){
k2=0;
for(j=0;j<13;j++){
if(j%4==0)k2++;
if(j%4!=0){
if(w[i,j]!=L"")a[i-k1][j-k2]=int::Parse(w[i,j]);
if(w[i,j]==L"")a[i-k1][j-k2]=0;
}
}
}
}
}
}
k1=0;
for(i=0;i<13;i++){
if(i%4==0)k1++;
if(i%4!=0){
k2=0;
for(j=0;j<13;j++){
if(j%4==0)k2++;
if(j%4!=0){
if(a[i-k1][j-k2]==0){
for(k=1;k<10;k++){
h=1;
if(j-k2>0){
for(l=0;l<j-k2;l++){
if(a[i-k1][l]==k){
h=0;
break;
}
}
}
if(h==1){
if(j-k2<8){
for(l=j-k2;l<9;l++){
if(a[i-k1][l]==k){
h=0;
break;
}
}
}
}
if(h==1){
a[i-k1][j-k2]=k;
dataGridView1[j,15+i]->Value=a[i-k1][j-k2];
}
}
}
}
}
}
}
}
}
};
}
解説
今回の核心部分は
k1=0;
for(i=0;i<13;i++){
if(i%4==0)k1++;
if(i%4!=0){
k2=0;
for(j=0;j<13;j++){
if(j%4==0)k2++;
if(j%4!=0){
if(a[i-k1][j-k2]==0){
for(k=1;k<10;k++){
h=1;
if(j-k2>0){
for(l=0;l<j-k2;l++){
if(a[i-k1][l]==k){
h=0;
break;
}
}
}
if(h==1){
if(j-k2<8){
for(l=j-k2;l<9;l++){
if(a[i-k1][l]==k){
h=0;
break;
}
}
}
}
if(h==1){
a[i-k1][j-k2]=k;
dataGridView1[j,15+i]->Value=a[i-k1][j-k2];
}
}
}
}
}
です。前に、
第24講 数独解答の作成☆
第1話 数独とは?
第2話 数独解答ソフト解答例
第3話 ブロック境界線解答例
第4話 ブロック重複判定部分解説
第5話 16次数独解答例
第6話 BackgroundWorkerによる高速化(9次の場合)
第7話 BackgroundWorkerによる高速化(9次の場合)の解説
で数独解答を作ったときは、関数の再帰的使用で作りましたが、
今回は、for文で作ってみました。
そして、成功したように見えます。
ですが、列の条件を加えると実はうまくいきません。
理由は、for文はすべての場合を調べ尽くしていないからです。
どうしてかは第11話で説明します。
ですから、結局は再帰版に作り直しますが、
このままfor文で行ってみます。
再帰版でつく直せば、一応数独の問題は解けるようになります。
ですが、超上級問題だと問題によっては解くのに数十分を要してしまいます。
Ver.1完成の後には、問題全体解析とそれに基づく番号再作成を加えます。
これがVer.2です。
さらに、問題全体解析から問題部分解析に変更していきVer.3、Ver.4、Ver.5、Ver.6、Ver.7へとバージョンアップを重ねていきます。
最初は問題の全体の解析が必要ですが、その後は全体解析は必要ありません。
数独(ナンバープレス)に数字を入れる度に、問題構造が変わっていきますが、
数字を新たに入れたことによって影響を受ける部分だけ解析し直すのが問題部分解析です。
ところが、この部分解析は非常な困難を伴うので、少しずつ改良していくしかありません。
それで、バージョンが細かく分かれます。
最速のVer.7まで進化した段階で、初めて本講義の最終講義である数独(ナンバープレイス)問題作成ソフトの制作に入ります。
解答を作ってから、そこから空欄を作っていくわけですが、
解答の並びによって、問題の難度は決まってしまっています。
つまり、解答の並びによって難易度は決まるのであって、決して空欄の作り方のよって決まるのではないのです。
解答の並び方が悪ければ、どのように空欄を作ったとしても決して難度を上げることは出来ません。
無理に難度を上げると、答えが複数存在するようになってしまうからです。
数独(ナンバープレス)問題作成には、3つの要求をクリアしなければなりません。
ⅰ 解が存在しなければならない。
ⅱ 解は唯一解でなければならない。
ⅲ 難度が一定以上でなければならない。
このⅱとⅲが互いに矛盾しあう要求なのです。
ⅱとⅲは、難度を上げると答えが複数存在するようになってしまう、しかし答えを1つに限定すると難度が下がってしまう、
という緊張関係にあります。
ここに数独(ナンバープレス)問題作成の難しさがあります。
適当に入れたのでは、答えが存在しなくなります。
つまり、ⅰの条件を満たさないのです。
したがって、解答から問題を作るしかないのですが、
その際にⅱとⅲが衝突します。
面白い問題を作るには、結局試行錯を誤繰り返すしかありません。
1秒で数千というレベルで試行錯誤を繰り返さない限り、良問はできあがりません。
ですから、解答作りは最速でなければならないのです。
0.0001秒という単位で解答を作り出さなければならないです。
さて、解説に戻りましょう。
なぜ、すべての場合をもらするのに4次元すなわちもとに2次元にさらに2次元を加えなければならないのでしょうか。
うっかりすると、次の3次元プログラムを考えてしまうのではないでしょうか。
k1=0;
for(i=0;i<13;i++){
if(i%4==0)k1++;
if(i%4!=0){
k2=0;
h=1;
for(j=0;j<13;j++){
if(j%4==0)k2++;
if(j%4!=0){
if(a[i-k1][j-k2]==0){
if(j-k2>0){
for(k=0;k<j-k2;k++){
if(a[i-k1][k]==j+1){
h=0;
break;
}
}
}
if(h==1){
a[i-k1][j-k2]=j+1;
dataGridView1[j,15+i]->Value=a[i-k1][j-k2];
}
}
}
}
}
}
ところが、これだと
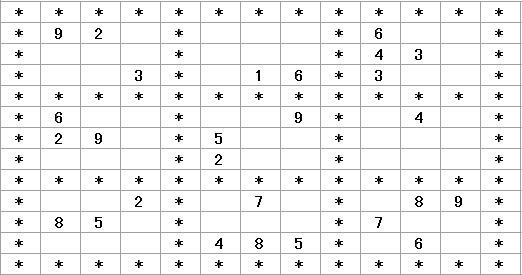
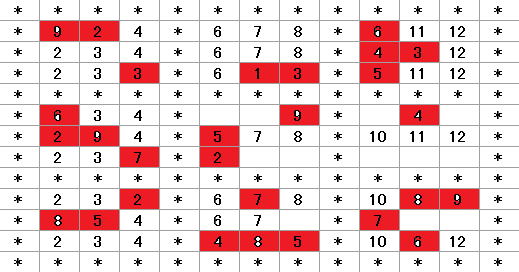
となってしまします。
まず、a[i-k1][k]==j+1;がおかしいですね。
a[i-k1][k]==j-k2+1;でなければなりませんね。でもそのように改良したとしても、
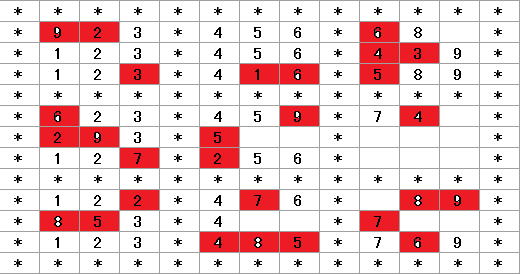
と実行結果は悲惨なものです。
この過ちは、私が起こしたものを再現しています。
何がおかしいのでしょうか。
第7話へ 第9話へ
