前話解答例
pragma once
int a[5][5],b[5][5],i,j;
namespace while文による2次元ループ {
using namespace System;
・
・
・
#pragma endregion
String^ w=L"";
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
f1(); //データ1発生
f2(); //データ1表示
f3(); //データ2発生
f4(); //データ2表示
f5(); //データ1とデータ2の和の計算と表示
}
void f1(void){
i=0;
while(i<5){
j=0;
while(j<5){
a[i][j]=5*i+j+1;
j++;
}
i++;
}
}
void f2(void){
i=0;
while(i<5){
j=0;
while(j<5){
if(a[i][j]<10)w+=L"0"+(a[i][j]).ToString()+L" ";
if(a[i][j]>=10)w+=(a[i][j]).ToString()+L" ";
j++;
}
w+=L"\n";
i++;
}
label1->Text=w;
}
void f3(void){
i=0;
while(i<5){
j=0;
while(j<5){
b[j][i]=5*i+j+1;
j++;
}
i++;
}
}
void f4(void){
i=0;
w=L"";
while(i<5){
j=0;
while(j<5){
if(b[i][j]<10)w+=L"0"+(b[i][j]).ToString()+L" ";
if(b[i][j]>=10)w+=(b[i][j]).ToString()+L" ";
j++;
}
w+=L"\n";
i++;
}
label2->Text=w;
}
void f5(void){
i=0;
w=L"";
while(i<5){
j=0;
while(j<5){
if(a[i][j]+b[i][j]<10)w+=L"0"+(a[i][j]+b[i][j]).ToString()+L" ";
if(a[i][j]+b[i][j]>=10)w+=(a[i][j]+b[i][j]).ToString()+L" ";
j++;
}
w+=L"\n";
i++;
}
label3->Text=w;
}
};
}
さて、今回はローカル変数のみを利用した簡単なソフトを2つ作り、
関数の独立性の意味を考えてみましょう。
まず、1番目のソフトから。
Form1
ソースコード
#pragma endregion
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
int a;
a=5;
f();
g();
h();
label1->Text=a.ToString();
}
void f(void){
int a;
a=8;
label2->Text=a.ToString();
}
void g(void){
int a;
a=1;
label3->Text=a.ToString();
}
void h(void){
int a;
a=7;
label4->Text=a.ToString();
}
};
}
実行結果

プログラムは上から下へと流れます。
int a;
a=5;
この2行の後、f();が実施されるので
int a;
a=8;
label2->Text=a.ToString();
の3行が実施されます。もし、関数の独立性がなければここでエラーしてしまいます。
なぜならint a; が重複して宣言されるからです。仮にint a; がなく
a=5;
としても、関数の独立性のためにSystem::Void button1_Clickのaの値は書き換えられません。
次に、g();が実行され
int a;
a=1;
label3->Text=a.ToString();
の3行が、さらにh();が実行され
int a;
a=7;
label4->Text=a.ToString();
の3行の処理が行われ、最後に
label1->Text=a.ToString();
が実施されますが、label1の実行結果を見れば、
aの内容が、他の関数によって書き換えられていないことがわかります。
つまり、同じ変数aであっても、それぞれの有効範囲は関数の中のみなので、つまりローカル変数なので、
書き換えられる心配がないわけです。
したがって、プログラマーは自分の担当箇所だけの開発に専念すればよいことになります。
もし、独立性がなければ他の箇所にも気を配りながら開発しなければならなくなります。
今回のソフトは、f(){ }、g(){ }、h(){ }において部品が用意され、
メインプログラムであるSystem::Void button1_Click(・・・){・・・}においてそれらの部品が組み立てられています。
このように独立部品を組み立てて、全体をプログラミングすることを構造化プログラミングというのです。
構造化プログラミングは、プログラムがわかりやすいだけではありません。
各関数は終了すると同時にメモリから消滅します。
ということは、関数の中のローカル変数もメモリから消滅します。
関数は、呼び出されれば発生し、終わると消滅するという生成消滅を繰り返します。
消滅によって、メモリの大幅な節約ができます。
尚、System::Void button1_Click(・・・){・・・}は、f()、g()、h()が消滅した後もまだ生きています。
まだ、すべての処理を終えず現在進行形だからです。
そして、最後の処理
label1->Text=a.ToString();
が行われて全行程を終了して初めて消滅します。
グローバル変数は、プログラム実行中はメモリに常駐しますので、
グローバル変数を多用しすぎると、メモリが不足する事態にもなるのです。
もっとも、現在のパソコンのメモリは昔の何十万倍以上ありますから、
1万個グローバル変数を用意しようと、メモリはまだまだ余裕があります。
ですから、初心者の方はグローバル変数を使っても何の差し障りもないことになります。
ですが、将来大きなプログラムを組むことを考えてなるべくローカル変数にするようにした方がよいことも事実です。
2例目は、もう少し複雑なソフトを組んでみましょう。
Form1
コーティング
#pragma endregion
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
f1(); //1から100までの整数の和
f2(); //2から100までの偶数の和
f3(); //1から100までの整数の2乗の和
f4(); //2から100までの偶数の2乗の和
}
void f1(void){
int i,w
w=0;
for(i=1;i<51;i++){
w+=i;
}
textBox1->Text=w.ToString();
}
void f2(void){
int i,w;
w=0;
for(i=2;i<101;i+=2){
w+=i;
}
textBox2->Text=w.ToString();
}
void f3(void){
int i,w;
w=0;
for(i=1;i<101;i++){
w+=i*i;
}
textBox3->Text=w.ToString();
}
void f4(void){
int i,w;
w=0;
for(i=2;i<101;i+=2){
w+=i*i;
}
textBox4->Text=w.ToString();
}
};
}
実行例
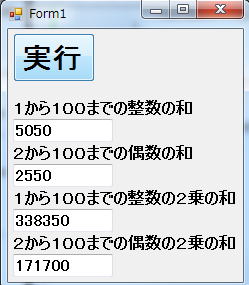
関数の独立性のため各関数ごとに計4回もint i,w; を宣言しています。
したがいまして、むしろこの例だと不便なように思えます。
ですが、この例においても関数の便利さがわかります。
例えば、5人でも分業が可能になります。
Void button1_Click、f1()、f2()、f3()、f4()の担当者が他の部分をまったく気にしないでプログラムの開発に専念できるからです。
また、変数名で頭を悩ませる必要がありません。
関数の独立性が如何に便利であるかは次のようにコーティングを変更するとわかります。
#pragma endregion
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
f1();//1から100までの整数の和
f3();//1から100までの整数の2乗の和
f4();//2から100までの偶数の2乗の和
}
void f1(void){
int i,w;
w=0;
for(i=1;i<51;i++){
w+=i;
}
f2();//2から100までの偶数の和 f2においてwが使われていても何の影響もない。
for(i=51;i<101;i++){
w+=i;
}
textBox1->Text=w.ToString();
}
void f2(void){
int i,w;
w=0;
for(i=2;i<101;i+=2){
w+=i;
}
textBox2->Text=w.ToString();
}
void f3(void){
int i,w;
w=0;
for(i=1;i<101;i++){
w+=i*i;
}
textBox3->Text=w.ToString();
}
void f4(void){
int i,w;
w=0;
for(i=2;i<101;i+=2){
w+=i*i;
}
textBox4->Text=w.ToString();
}
};
}
実行結果

では皆さん、上を参考に
#pragma endregion
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
f1();//1から100までの整数の和
}
でも同様な結果が出るようにプログラミングして下さい。
もちろん、今回同様に半分までの和を前半でやり、中にf3などを挟み、
さらに和を再開させて最後まで求めるが条件です。
答えは30行下。
#pragma endregion
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
f1();//1から50までの整数の和
}
void f1(void){
int i,w;
w=0;
for(i=1;i<51;i++){
w+=i;
}
f2();//2から100までの偶数の和 f2においてwが使われていても何の影響もない。
for(i=51;i<101;i++){
w+=i;
}
textBox1->Text=w.ToString();
}
void f2(void){
int i,w;
w=0;
for(i=2;i<51;i+=2){
w+=i;
}
f3();//1から100までの整数の2乗の和 f3においてwが使われていても何の影響もない。
for(i=52;i<101;i+=2){
w+=i;
}
textBox2->Text=w.ToString();
}
void f3(void){
int i,w;
w=0;
for(i=1;i<51;i++){
w+=i*i;
}
f4();//2から100までの偶数の2乗の和 f4においてwが使われていても何の影響もない。
for(i=51;i<101;i++){
w+=i*i;
}
textBox3->Text=w.ToString();
}
void f4(void){
int i,w;
w=0;
for(i=2;i<101;i+=2){
w+=i*i;
}
textBox4->Text=w.ToString();
}
};
}
実行結果

変数名が同じでも他の関数で侵犯されたり、浸食されることがないので、その関数のみの開発に専念できるのです。
さて、課題を出して今話を閉じます。
コーティングを
#pragma endregion
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
f1(); //1から100までの整数の和
f2(); //2から100までの偶数の和
f3(); //1から100までの整数の2乗の和
f4(); //2から100までの偶数の2乗の和
}
void f1(void){
int i,w
w=0;
for(i=1;i<51;i++){
w+=i;
}
textBox1->Text=w.ToString();
}
void f2(void){
int i,w;
w=0;
for(i=2;i<101;i+=2){
w+=i;
}
textBox2->Text=w.ToString();
}
void f3(void){
int i,w;
w=0;
for(i=1;i<101;i++){
w+=i*i;
}
textBox3->Text=w.ToString();
}
void f4(void){
int i,w;
w=0;
for(i=2;i<101;i+=2){
w+=i*i;
}
textBox4->Text=w.ToString();
}
};
}に戻した上で、Form1を
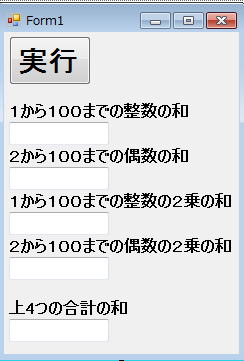
のように改造して、4つの合計の和が求めら得るようにしてみてください。
ただし、4つの合計の和を求める際、各textBoxから値を取得してはならないという条件を付け加えます。
この課題を成就するには、
int f1(void){
・
・
・
retrn w;
}
として、合計値を戻しましょう。
したがいまして、
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
f1(); //1から100までの整数の和
f2(); //2から100までの偶数の和
f3(); //1から100までの整数の2乗の和
f4(); //2から100までの偶数の2乗の和
}
の方も、
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
int w1,w2,w3,w4;
w1=f1(); //1から100までの整数の和
w2=f2(); //2から100までの偶数の和
・
・
・
}
のように変更しなければなりません。
第1話へ 第3話へ
