第6講 ポインタの学習
第3話 多次元配列が1次元配列やポインタで表せる理由
前話解答例
#pragma endregion
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^
e) {
//ポインタの宣言
int* a;
//変数の宣言
int i,j;
//ポインタの初期化(メモリ割り当て)
a=(int *)malloc;
//ポインタに内容を代入
for(i=0;i<20;i++)*(a+i)=2*i+1;
//文字変数の宣言
String^ w=L"";
//配列の宣言
int b[4][5],c[5][4],d[10][2];
//ポインタのb[4][5]への代入
for(i=0;i<4;i++){
for(j=0;j<5;j++){
b[i][j]=*(a+5*i+j);
}
}
//b[4][5]の内容の表示
for(i=0;i<4;i++){
for(j=0;j<5;j++){
if(b[i][j]<10)w=w+L"0"+(b[i][j]).ToString()+L"
";
if(b[i][j]>=10)w=w+(b[i][j]).ToString()+L" ";
}
w=w+L"\n";
}
label1->Text=w;
//ポインタのc[5][4]への代入
for(i=0;i<5;i++){
for(j=0;j<4;j++){
c[i][j]=*(a+4*i+j);
}
}
//c[5][4]の内容の表示
w=L"";
for(i=0;i<5;i++){
for(j=0;j<4;j++){
if(c[i][j]<10)w=w+L"0"+(c[i][j]).ToString()+L"
";
if(c[i][j]>=10)w=w+(c[i][j]).ToString()+L" ";
}
w=w+L"\n";
}
label2->Text=w;
//ポインタのd[10][2]への代入
for(i=0;i<10;i++){
for(j=0;j<2;j++){
d[i][j]=*(a+2*i+j);
}
}
//b[4][5]の内容の表示
w=L"";
for(i=0;i<10;i++){
for(j=0;j<2;j++){
if(d[i][j]<10)w=w+L"0"+(d[i][j]).ToString()+L"
";
if(d[i][j]>=10)w=w+(d[i][j]).ToString()+L" ";
}
w=w+L"\n";
}
label3->Text=w;
}
};
}
次話では、ポインタのポインタを話題にしますが、その前に何故多次元配列が1次元配列やポインタで表せるかを説明していきましょう。
例えば、
int b[2][3];
の場合データは次のよう2次元に並びます。
| b[0][0] |
b[0][1] |
b[0][2] |
| b[1][0] |
b[1][1] |
b[1][2] |
ですがメモリはどのように配置されているかと申しますと、
| アドレス |
00000000 |
0000004 |
00000008 |
00000012 |
0000016 |
00000016 |
| 配列 |
b[0][0] |
b[0][1] |
b[0][2] |
b[1][0] |
b[1][1] |
b[1][2] |
と直線的に並んでいます。結局2次元配列とは本来的には、1次元データ(直線的データ)を見かけだけ2次元にしたものに過ぎません。
ですから、ポインタと次のように対応させることができます。
| 配列 |
b[0][0] |
b[0][1] |
b[0][2] |
b[1][0] |
b[1][1] |
b[1][2] |
| ポインタ |
*a |
*(a+1) |
*(a+2) |
*(a+3) |
*(a+4) |
*(a+5) |
と対応させることができます。また、この表からb[i][j]=*(a+3*i+j)であることもわかります。
| 配列 |
b[0][0] |
b[0][1] |
b[0][2] |
b[1][0] |
b[1][1] |
b[1][2] |
| ポインタ |
*a(3*0+0) |
*(a+3*0+1) |
*(a+3*0+2) |
*(a+3*1+0) |
*(a+3*1+1) |
*(a+3*1+2) |
がわかります。もちろん1次元配列でも同じです。
| 2次元 |
b[0][0] |
b[0][1] |
b[0][2] |
b[1][0] |
b[1][1] |
b[1][2] |
| 1次元 |
a[3*0+0)] |
a[3*0+1] |
a[3*0+2] |
a[3*1+0] |
a[3*1+1] |
a[3*1+2] |
つまり、b[i][j]=a[3*i+j]です。
また、3次元配列の場合も
int b[4][2][3];
を例にするなら
| 配列 |
b[0][0][0] |
b[0][0][1] |
b[0][0][2] |
b[0][1][0] |
b[0][1][1] |
b[0][1][2] |
| ポインタ |
*(a+6*0+3*0+0) |
*(a+6*0+3*0+1) |
*(a+6*0+3*0+2) |
*(a+6*0+3*1+0) |
*(a+6*0+3*1+1) |
*(a+6*0+3*1+2) |
| 配列 |
b[1][0][0] |
b[1][0][1] |
b[1][0][2] |
b[1][1][0] |
b[1][1][1] |
b[1][1][2] |
| ポインタ |
*(a+6*1+3*0+0) |
*(a+6*1+3*0+1) |
*(a+6*1+3*0+2) |
*(a+6*1+3*1+0) |
*(a+6*1+3*1+1) |
*(a+6*1+3*1+2) |
| 配列 |
b[2][0][0] |
b[2][0][1] |
b[2][0][2] |
b[2][1][0] |
b[2][1][1] |
b[2][1][2] |
| ポインタ |
*(a+6*2+3*0+0) |
*(a+6*2+3*0+1) |
*(a+6*2+3*0+2) |
*(a+6*2+3*1+0) |
*(a+6*2+3*1+1) |
*(a+6*2+3*1+2) |
| 配列 |
b[3][0][0] |
b[3][0][1] |
b[3][0][2] |
b[3][1][0] |
b[3][1][1] |
b[3][1][2] |
| ポインタ |
*(a+6*3+3*0+0) |
*(a+6*3+3*0+1) |
*(a+6*3+3*0+2) |
*(a+6*3+3*1+0) |
*(a+6*3+3*1+1) |
*(a+6*3+3*1+2) |
| 3次元 |
b[0][0][0] |
b[0][0][1] |
b[0][0][2] |
b[0][1][0] |
b[0][1][1] |
b[0][1][2] |
| 1次元 |
a[6*0+3*0+0] |
a[6*0+3*0+1] |
a[6*0+3*0+2] |
a[6*0+3*1+0] |
a[6*0+3*1+1] |
a[6*0+3*1+2] |
| 3次元 |
b[1][0][0] |
b[1][0][1] |
b[1][0][2] |
b[1][1][0] |
b[1][1][1] |
b[1][1][2] |
| 1次元 |
a[6*1+3*0+0] |
a[6*1+3*0+1] |
a[6*1+3*0+2] |
a[6*1+3*1+0] |
a[6*1+3*1+1] |
a[6*1+3*1+2] |
| 3次元 |
b[2][0][0] |
b[2][0][1] |
b[2][0][2] |
b[2][1][0] |
b[2][1][1] |
b[2][1][2] |
| 1次元 |
a[6*2+3*0+0] |
a[6*2+3*0+1] |
a[6*2+3*0+2] |
a[6*2+3*1+0] |
a[6*2+3*1+1] |
a[6*2+3*1+2] |
| 3次元 |
b[3][0][0] |
b[3][0][1] |
b[3][0][2] |
b[3][1][0] |
b[3][1][1] |
b[3][1][2] |
| 1次元 |
a[6*3+3*0+0] |
a[6*3+3*0+1] |
a[6*3+3*0+2] |
a[6*3+3*1+0] |
a[6*3+3*1+1] |
a[6*3+3*1+2] |
(本当は直線上に並んでいますが、画面上に入らないので2次元表示になっています。)
したがって、
b[i][j][k]=*(a+6*i+3*j+k)ないしはb[i][j][k]=a[6*i+3*j+k]の対応がわかります。
それでは課題を出してこの話を閉じましょう。
ポインタ a=(int *)malloc;と3次元配列int b[3][4][5];を宣言し、
データをfor(i=0;i<60;i++)*(a+i)=i+1;のようにポインタ側に発生させて、
それを3次元配列の代入して実行画面が
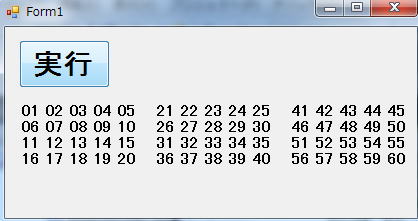
となるようにしましょう。
ただし、for文による3次元ループでこれを実現することを条件とします。
その際に、
for(i=0;i<60;i++)labeli->Text=w;
のような使い方はできませんので、
表示についてはif文で工夫して下さい。
第2話へ 第4話へ

vc++講義へ
vb講義へ
VB講義基礎へ
初心者のための世界で一番わかりやすいVisual Basic入門基礎講座へ
数学研究室に戻る

