３．Ｃ＝１２０°の場合
ここで，
ｘ＝ｚ－α，ｙ＝β－ｚとおくと，
これを展開してｚについて整理すると，
これはＣ＝６０°の場合と全く同じ式である。
以下の議論もほとんど同じになるが，ｙの置き方が違っているので若干異なる。
ここで，α＋β＝０のとき，α＝０またはβ＝０であるが，β＝０とするとｙ＝－ｚとなり，ｙ，ｚが正の有理数であるという仮定に反する。α＝０とすると，ｘ＝ｚとなりＣと底角とする２等辺三角形になるが，これはＣ＝１２０°に反する。よって，α＋β≠０
したがって，
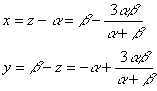
以下方法は２つある。一つは，Ｃ＝６０°の場合を踏襲する方法（Ⅰ）であり，もう一つは分母α＋βが約分によって消えるようにしてやる方法（Ⅱ）である。
Ⅰ Ｃ＝６０°の場合を踏襲する方法
それぞれの両辺にα＋βをかけると，
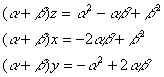Ａ
（α＋β）ｚ，（α＋β）ｘ，（α＋β）ｙをそれぞれ，ｚ，ｘ，ｙと置き直すと，
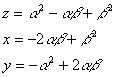
ｚ＞０，ｘ＞０，ｙ＞０の条件からβ＞０ならば０＜α＜β／２であり，β＜０ならばβ／２＜α＜０
したがって，
となり，ｘ，ｙ，ｚは三角条件を満たしている。β≠０であるので，正の有理数解（ｘ，ｙ，ｚ）は無限に存在することすなわち自然数解（ｘ，ｙ，ｚ）は無限に存在することが示された。
Ⅱ 分母α＋βが約分によって消えるようにしてやる方法
（ｐ，ｑ，ｒは適当な有理数）とおいて，分母が消えるようにｐ，ｑ，ｒの値を決める。Ａの式に代入すると，
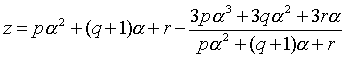
後半のわり算
を実行すると，商が
で余りが
である。よって，割り切れるための条件は，ｑ＝－１，ｒ＝０である。このとき，
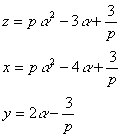
両辺をｐ倍して、それぞれを改めてｚ、ｘ、ｙとおくと
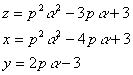
よって，ｐ＞０のときは十分大きいαに対してｚ＞０，ｘ＞０，ｙ＞０であり、ｐ＜０のときは十分小さいαに対してｚ＞０，ｘ＞０，ｙ＞０である。
また，
より，ｐ＞０のときは十分大きいαに対してｘ＋ｙ－ｚ＞０であり、ｐ＜０のときは十分小さいαに対してｘ＋ｙ－ｚ＞０を満たし，ｘ，ｙ，ｚは三角条件を満たしている。
以上より自然数解（ｘ，ｙ，ｚ）は無限に存在していることが示された。いくつかの解を示してみよう。
①
ｐ＝１のとき
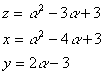
ⅰ α＝４とすると
ｚ＝７，ｘ＝３，ｙ＝５
よって，（３，５，７）
ⅱ α＝５とすると
ｚ＝１３，ｘ＝８，ｙ＝７
よって，（ｘ，ｙ，ｚ）＝（８，７，１３）
ⅲ α＝６とすると，
ｚ＝２１，ｘ＝１５，ｙ＝９
よって，（ｘ，ｙ，ｚ）＝（５，３，７）
ⅳ α＝７とすると，
ｚ＝３１，ｘ＝２４，ｙ＝１１
よって，（ｘ，ｙ，ｚ）＝（２４，１１，３１）
ⅴ α＝８とすると，
ｚ＝４３，ｘ＝３５，ｙ＝１３
よって，（ｘ，ｙ，ｚ）＝（３５，１３，４３）
ⅵ α＝９とすると，
ｚ＝５７，ｘ＝４８，ｙ＝１５
よって，（ｘ，ｙ，ｚ）＝（１６，５，１９）
②
ｐ＝２のとき
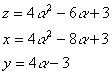
ⅰ α＝３とすると，
ｚ＝２１，ｘ＝１５，ｙ＝９
よって，（ｘ，ｙ，ｚ）＝（５，３，７）
ⅱ α＝４とすると，
ｚ＝４３，ｘ＝３５，ｙ＝１３
よって，（ｘ，ｙ，ｚ）＝（３５，１３，４３）
ⅲ α＝５とすると，
ｚ＝７３，ｘ＝６３，ｙ＝１７
よって，（ｘ，ｙ，ｚ）＝（６３，１７，７３）
ⅳ α＝６とすると，
ｚ＝１１１，ｘ＝９９，ｙ＝２１
よって，（ｘ，ｙ，ｚ）＝（３３，７，３７）
ⅴ α＝７とすると，
ｚ＝１５７，ｘ＝１４３，ｙ＝２５
よって，（ｘ，ｙ，ｚ）＝（１４３，２５，１５７）
ⅵ α＝８とすると，
ｚ＝２１１，ｘ＝１９５，ｙ＝２９
よって，（ｘ，ｙ，ｚ）＝（１９５，２９，２１１）
①
②は重複があるが，明らかに違う無限系列を作り出している。βの値によって無限系列が異なるので，無限系列は無限種類存在することになる。
