4.t≠1/2,t≠0,-1<t<1の場合
![]()
ここで,
x=z-α,y=z-βとおくと,
![]()
これを展開してzについて整理すると,
![]()
よって,t≠1/2ならば
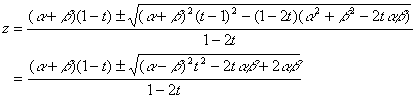 A
A
このような複雑な式からルートが消え,しかも約分によって分母も消えてしまうものなのだろうか?
t=-1/2の場合を手がかかりにしてみよう。
t=-1/2とおくと,
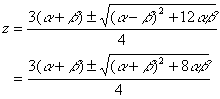 B
B
Ⅱ分母α+βが約分によって消えるようにしてやる方法では任意の整数pに対して,
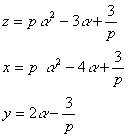
であった。このとき,
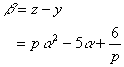
これを式Bに代入すると,
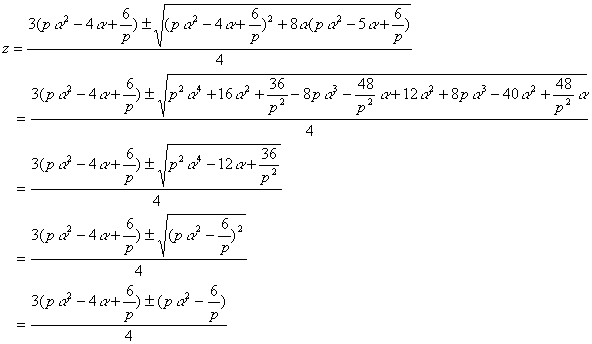
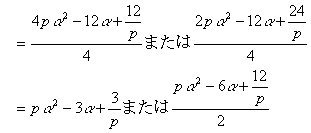
魔法のようにルートがはずれ,しかも一方の場合は分母まで消えている!!!
どうやらポイントは,βをαの2次式に置くことにあるようである。
![]()
において,
![]()
とおいてみよう。さらに,ルートの中をDとおくと,
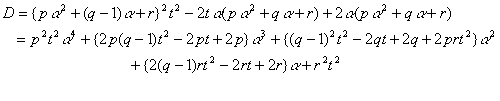 ここで,
ここで,
![]()
![]() =0
=0
とおくと,
![]()
であり,
![]()
ここで,
![]()
とおくと,
![]()
であり,式Cが完全平方になるための条件は,
![]()
すなわち,
![]()
![]() より,
より,
![]()
すなわち,
![]()
このとき,
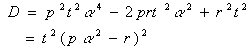
したがって,
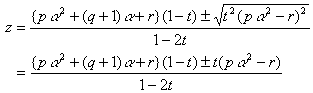
よって,一方は
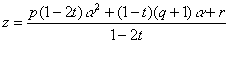
ここで,![]() を代入すると,
を代入すると,
![]()
x=z-α,y=z-βより
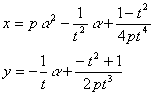
ゆえに,t>0のときは十分小さいαに対して,t<0のときは十分大きいαに対して,z>0,x>0,y>0を満たし,最大辺はzまたはxである。しかも,
|z-x|=|α|<y
したがって,x,y,zは三角条件を満たす。
以上より,正の有理数解(x,y,z)は無限に存在する。すなわち,自然数解(x,y,z)が無限に存在する。
t=1/3,-3/7についていくつかの解を示してみよう。
t=1/3のとき
p=1の場合
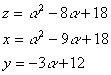
ⅰ α=2とすると
z=6,x=4,y=6
よって,(x,y,z)=(2,3,3)
ⅱ α=1とすると
z=11,x=10,y=9
よって,(x,y,z)=(10,9,11)
ⅲ α=0とすると,
z=18,x=18,y=12
よって,(x,y,z)=(3,2,3)
ⅳ α=-1とすると,
z=27,x=28,y=15
よって,(x,y,z)=(28,15,27)
ⅴ α=-2とすると,
z=38,x=40,y=18
よって,(x,y,z)=(20,9,19)
ⅵ α=-3とすると,
z=51,x=54,y=21
よって,(x,y,z)=(18,7,17)
p=2のとき
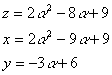
ⅰ α=1とすると,
z=3,x=2,y=3
よって,(x,y,z)=(2,3,3)
ⅱ α=0とすると,
z=9,x=9,y=6
よって,(x,y,z)=(3,2,3)
ⅲ α=-1とすると,
z=19,x=20,y=9
よって,(x,y,z)=(20,9,19)
ⅳ α=-2とすると,
z=33,x=35,y=12
よって,(x,y,z)=(35,12,33)
ⅴ α=-3とすると,
z=51,x=54,y=15
よって,(x,y,z)=(18,5,17)
ⅵ α=-4とすると,
z=73,x=18,y=73
よって,(x,y,z)=(77,29,73)
①②は重複があるが,明らかに違う無限系列を作り出している。pの値によって無限系列が異なるので,無限系列は無限種類存在することになる。
t=-3/7のとき
p=1とする。
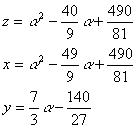
すべての両辺に81をかけて,改めてz,x,yとおくと,
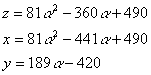
ⅰ α=4とすると,
z=346,x=22,y=336
よって,(x,y,z)=(11,168,173)
ⅱ α=5とすると,
z=715,x=310,y=525
よって,(x,y,z)=(62,105,143)
ⅲ α=6とすると,
z=1246,x=760,y=714
よって,(x,y,z)=(380,357,623)
