２．Ｃ＝０°の場合
ここで，
ｘ＝ｚ－α，ｙ＝ｚ－βとおくと，
これを展開してｚについて整理すると，
よって，
ここで，
とおけば，
ｎを定数とみた場合少なくとも，
は十分大きいｍに対してｚ＞０，ｘ＞０，ｙ＞０を満たすことは明らかである。
また，
であり，ｘ，ｙ，ｚは三角条件を満たしている。
以上より，ピタゴラス数は無数に存在することが示された。
具体的な値を求めてみよう。
①
ｎ＝１のとき
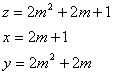
ⅰ ｍ＝１とすると
ｚ＝５，ｘ＝３，ｙ＝４
よって，（ｘ，ｙ，ｚ）＝（３，４，５）
ⅱ ｍ＝２とすると
ｚ＝１３，ｘ＝５，ｙ＝１２
よって，（ｘ，ｙ，ｚ）＝（５，１２，１３）
ⅲ ｍ＝３とすると，
ｚ＝２５，ｘ＝７，ｙ＝２４
よって，（ｘ，ｙ，ｚ）＝（７，２４，２５）
ⅳ ｍ＝４とすると，
ｚ＝４１，ｘ＝９，ｙ＝４０
よって，（ｘ，ｙ，ｚ）＝（９，４０，４１）
ⅴ ｍ＝５とすると，
ｚ＝６１，ｘ＝１１，ｙ＝６０
よって，（ｘ，ｙ，ｚ）＝（１１，６０，６１）
ⅵ ｍ＝６とすると，
ｚ＝８５，ｘ＝１３，ｙ＝８４
よって，（ｘ，ｙ，ｚ）＝（１３，８４，８５）
②
ｎ＝２のとき
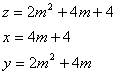
ⅰ ｍ＝１とすると，
ｚ＝１０，ｘ＝８，ｙ＝６
よって，（ｘ，ｙ，ｚ）＝（４，３，５）
ⅱ ｍ＝２とすると，
ｚ＝２０，ｘ＝１２，ｙ＝１６
よって，（ｘ，ｙ，ｚ）＝（３，４，５）
ⅲ ｍ＝３とすると，
ｚ＝３４，ｘ＝１６，ｙ＝３０
よって，（ｘ，ｙ，ｚ）＝（８，１５，１７）
ⅳ ｍ＝４とすると，
ｚ＝５２，ｘ＝２０，ｙ＝４８
よって，（ｘ，ｙ，ｚ）＝（５，１２，１３）
ⅴ ｍ＝５とすると，
ｚ＝７４，ｘ＝２４，ｙ＝７０
よって，（ｘ，ｙ，ｚ）＝（１２，３５，３７）
ⅵ ｍ＝６とすると，
ｚ＝１００，ｘ＝２８，ｙ＝９６
よって，（ｘ，ｙ，ｚ）＝（７，２４，２５）
①
と②は重複があるが，明らかに違う無限系列を作り出している。ｎの値によって無限系列が異なるので，無限系列は無限種類存在することになる。
