すべての行(横)の合計、
すべての列(縦)の合計、
2本の対角線の合計を同じくしてやることが出来ます。
これを利用して、魔方陣を作成させる方法が細胞構成法です。
詳しくは、小学生・中学生のための魔方陣授業(初歩から最新研究まで)の第19回 細胞構成法第1弾(6次魔方陣に挑戦!)
を参照してください。
VBAで作った魔方陣(細胞構成法)をまずご覧になってください。
VBAですから、当然シングルスレッド(VBAは基本的にマルチスレッドは出来ない)です。
したがって、CPUを4つ積んでいるタイプでは、CPU使用率は約25%程度にすぎませんが、
非常に高速であることがわかります。おそらく、私が作った魔方陣作成ソフトでは、
最速なのではないかと思います。
最初、シングルスレッドでVC++に魔方陣を作らせることを考えた上で、
BackgroundWorkerを使い、4スレッドにしていきましょう。
特に高速にするためには、末項確定法と組み合わせるのがよいでしょう。
末項確定法については
第21講 末項確定法△
第1話 末項確定法とは?
第2話 f1解答例と簡単な解説
第3話 f2解答例
第4話 末講確定法最適乱数系列探索ソフトプログラム例(前半)
第5話 末講確定法最適乱数系列探索ソフトプログラム例(後半)
第6話 末確定法の改良の試み
を参照して下さい。
最初からの開発では大変ですから
参考ファイルForm1.h へのリンク
を改良していきましょう。
まず、VC++を起動して、新しいプロジェクトを選びます。
名前を例えば、『細胞確定法』とします。
(もし、全角文字だと問題が起きる環境の場合は、半角英数で適切な名前にしてください。)
そして、OKをします。
ソリューションエクスプローラ
 (画面は、名前を細胞構成法とした場合で例示)のForm1.hを右クリックしコードの表示を選びます。
(画面は、名前を細胞構成法とした場合で例示)のForm1.hを右クリックしコードの表示を選びます。上から下までドラッグして、
 Deleteキー押して、いったすべて消します。
Deleteキー押して、いったすべて消します。参考ファイルForm1.h へのリンクをダブルクリックして開いて、上から下までドラッグによって範囲を指定し、右クリック→コピーをします。
VC++のコードで右クリック→貼り付けをします。
するとVC++のコードが
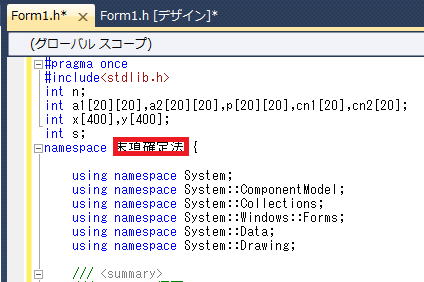 と変わります。
と変わります。そして、末項確定法の部分を自分で付けた名前(今回の例示
 の場合は、細胞構成法)にします。
の場合は、細胞構成法)にします。そして、F5でビルドすると、細胞構成法ソフトが立ち上がります。
ただし、名前は細胞構成法で、も実際には内容は末項確定法です。
参考ファイルForm1.h へのリンクのコードを貼り付けて作ったものだからです。
コードを改良して、細胞確定法ソフトにします。
まず、
#pragma endregion
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
label2->Text=L"";
DateTime^ hj=DateTime::Now;
n=int::Parse(textBox1->Text);
int h=1;
if(n<3 || n>=12){
label2->Text=L"TextBoxには3以上11以下の整数\r\nを入力し再度実行ボタンを\r\n押して下さい。";
h=0;
}
if(h==1){
s=0;
if(n%2==1)g1(n);
if(n%2==0)g2(n);
syokika();
if(n==3 || n==4)srand(0);
if(n==5)srand(5);
if(n==6)srand(28);
if(n==7)srand(31);
if(n==8)srand(597);
if(n==9)srand(3154);
if(n==10)srand(1114);
if(n==11)srand(3375);
f1(0);
・
・
・
の
f1(0);
の前に、細胞を作る関数の呼び出しを入れます。
その関数は、戻り値のないvoid型でよいでしょう。
