#pragma once
#include<stdlib.h>
int n;
int a1[20][20],a2[20][20],a3[20][20],p[20][20],cn1[20],cn2[20];
int x[400],y[400];
int s,ks;
char sbr[24][2][2];
char sb[2][2];
char sx[4],sy[4];
char cn;
・
・
・
#pragma endregion
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
label2->Text=L"";
DateTime^ hj=DateTime::Now;
n=int::Parse(textBox1->Text);
char h=1;
if(n<3 || n>14 || n%2==0){
label2->Text=L"TextBoxには3以上11以下の奇数\r\nを入力し再度実行ボタンを\r\n押して下さい。";
h=0;
}
if(h==1){
s=0;
if(n%2==1)g1(n);
if(n%2==0)g2(n);
syokika();
cn=0;
zhy();
sbs(0);
/*
int i,j,k;
for(i=0;i<cn*3+1;i++)dataGridView1->Rows->Add();
for(i=0;i<cn;i++){
for(j=0;j<2;j++){
for(k=0;k<2;k++){
dataGridView1[k,j+3*i]->Value =sbr[i][j][k];
}
}
}
dataGridView1[0,cn*3]->Value =cn;
if(n!=3 )f0(0);
if(n==3)f1(0);
*/
ks=0;
sbg(0);
/*
array<String^>^ w=gcnew array<String^>(15);
int i;
w[9]=n.ToString();w[10]=L"次";w[11]=L"魔";w[12]=L"方";w[13]=L"陣";w[14]=s.ToString();
for(i=0;i<8;i++)w[i]=L"";
dataGridView1->Rows->Add(w);
DateTime^ ow=DateTime::Now;
TimeSpan sa=ow->Subtract(*hj);
w[9]=L"時";w[10]=L"間";w[11]=L"計";w[12]=L"則";w[13]=L":";w[14]=(sa.TotalSeconds).ToString();
for(i=0;i<9;i++)w[i]=L"";
dataGridView1->Rows->Add(w);
*/
}
}
・
・
・
void sbg(int g){
if(ks==200)return;
int i,j,k,h,w,ii,iii;
ii=rand()%24;
for(i=0;i<24;i++){
iii=(ii+i)%24;
for(j=0;j<2;j++){
for(k=0;k<2;k++){
a3[2*y[g]+j][2*x[g]+k]=sbr[iii][j][k];
}
}
h=1;
if(g==n-1){
w=0;
for(j=0;j<2*n;j++){
w+=a3[j][j];
}
if(w!=5*n)h=0;
}
if(h==1){
if(g==2*n-2){
w=0;
for(j=0;j<2*n;j++){
w+=a3[j][2*n-1-j];
}
if(w!=5*n)h=0;
}
}
if(h==1){
if(y[g]==0 && x[g]==n-2){
for(j=0;j<2;j++){
w=0;
for(k=0;k<2*n;k++){
w+=a3[2*y[g]+j][k];
}
if(w!=5*n){
h=0;
break;
}
}
}
}
if(h==1){
if(x[g]==0 && y[g]==n-2){
for(j=0;j<2;j++){
w=0;
for(k=0;k<2*n;k++){
w+=a3[k][2*x[g]+j];
}
if(w!=5*n){
h=0;
break;
}
}
}
}
if(h==1){
if(g>2*n-2 && x[g]==n-1){
for(j=0;j<2;j++){
w=0;
for(k=0;k<2*n;k++){
w+=a3[2*y[g]+j][k];
}
if(w!=5*n){
h=0;
break;
}
}
}
}
if(h==1){
if(g>2*n-2 && y[g]==n-1){
for(j=0;j<2;j++){
w=0;
for(k=0;k<2*n;k++){
w+=a3[k][2*x[g]+j];
}
if(w!=5*n){
h=0;
break;
}
}
}
}
if(h==1){
if(g==n*n-2){
for(j=0;j<2;j++){
w=0;
for(k=0;k<2*n;k++){
w+=a3[k][2*x[g]+j];
}
if(w!=5*n){
h=0;
break;
}
}
}
}
if(h==1){
if(g==n*n-1){
for(j=0;j<2;j++){
w=0;
for(k=0;k<2*n;k++){
w+=a3[2*y[g]+j][k];
}
if(w!=5*n){
h=0;
break;
}
}
}
}
if(h==1){
if(g+1<n*n){
sbg(g+1);
}
else{
array<String^>^ w=gcnew array<String^>(15);
for(j=0;j<2*n;j++){
for(k=0;k<2*n;k++){
w[k]=(a3[j][k]).ToString();
}
dataGridView1->Rows->Add(w);
}
for(j=0;j<14;j++)w[j]=L"";
dataGridView1->Rows->Add(w);
ks++;
if(ks==200)return;
}
}
}
}
実行例
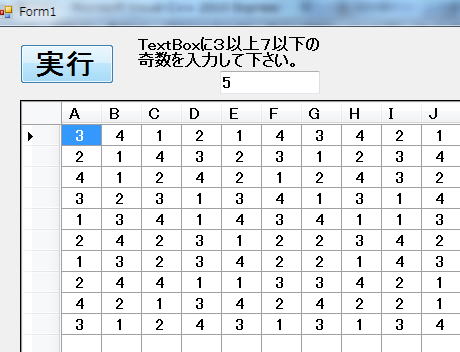
参考Form1.h
タイピングが面倒な方は、上のForm1.hをクリックして開いてコピーペースト(コピペ)で貼り付けてください。
今回も超難解ですね。解説は第12話以降でじっくり行います。
部品がすべてそろいました。
部品をうまく組み合わせて魔方陣の超高速作成に挑戦しましょう。
末項確定法の数万倍から数億倍は速いはずです。
末項確定法では、難しかった14次魔方陣が1個あたり0.01秒もかからず出来てしまうはずです。
第9話へ 第11話へ
