Thread^ A=gcnew Thread(gcnew ThreadStart(f)); を
Thread^ A=gcnew Thread(gcnew ParameterizedThreadStart(f)); にかえると、
A->Start(6); のように初めの値を送ることができます。
この値を受け取る関数側は、
static void f(Object^ 変数名)
のようにします。値を受け取るときの変数のタイプがObject^であると理解してください。
そして受け取るとき、例えば変数名がst、すなわち
static void f(Object^ st)なら、stを使うときは (Int32)st として使います。
つまり、Object^型を強制的にInt32型に変更して使うのです。
Int32型に変更すると、普通のint型の整数になります。
ですから、ParameterizedThreadStart使うと前の4スレッドは、
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
set<int> s;
int i,j,cn;
N=int::Parse(textBox1->Text);
s.clear();
s.insert(2);s.insert(3);s.insert(5);
for(i=0;i<cn1;i++){
s1[i]=0;
cn1=0;
}
for(i=0;i<cn2;i++){
s2[i]=0;
cn2=0;
}
for(i=0;i<cn3;i++){
s3[i]=0;
cn3=0;
}
for(i=0;i<cn4;i++){
s4[i]=0;
cn4=0;
}
DateTime^ hj=DateTime::Now; //開始時間
//スレッドの生成
Thread^ A=gcnew Thread(gcnew ParameterizedThreadStart(f));
Thread^ B=gcnew Thread(gcnew ParameterizedThreadStart(f));
Thread^ C=gcnew Thread(gcnew ParameterizedThreadStart(f));
Thread^ D=gcnew Thread(gcnew ParameterizedThreadStart(f));
//計算開始
A->Start(6);
B->Start(7);
C->Start(8);
D->Start(9);
//スレッドの終了を待つ
A->Join();
B->Join();
C->Join();
D->Join();
array<String^>^ w=gcnew array<String^>(10);
DateTime^ ow=DateTime::Now; //終了時間
for(i=0;i<=cn1;i++){
s.insert(s1[i]);
}
for(i=0;i<=cn2;i++){
s.insert(s2[i]);
}
for(i=0;i<=cn3;i++){
s.insert(s3[i]);
}
for(i=0;i<=cn4;i++){
s.insert(s4[i]);
}
cn=0;
for(set<int>::iterator it=s.begin();it!=s.end();it++){
if(*it==0)it++;
w[cn%10]=(*it).ToString();
if(cn==cn1+cn2+cn3+cn4+2){
for(j=(cn%10)+1;j<10;j++){
w[j]=L"";
}
}
if(cn%10==9)dataGridView1->Rows->Add(w);
cn++;
}
dataGridView1->Rows->Add(w);
TimeSpan sa=ow->Subtract(*hj); //経過時間の計算
w[0]=L"計算時間"; w[1]=sa.TotalSeconds.ToString();
for(i=2;i<10;i++)w[i]=L"";
dataGridView1->Rows->Add(w);
w[0]=L"素数個数"; w[1]=(cn1+cn2+cn3+cn4+3).ToString();
dataGridView1->Rows->Add(w);
}
static void f(Object^ st){
for (int i=(Int32)st; i<=N; i+=5) {
if(sh(i)){
if((Int32)st==6){
s1[cn1]=i;
cn1++;
}
if((Int32)st==7){
s2[cn2]=i;
cn2++;
}
if((Int32)st==8){
s3[cn3]=i;
cn3++;
}
if((Int32)st==9){
s4[cn4]=i;
cn4++;
}
}
}
}
static char sh(double n){
char h=1;
double a;
int b;
int c;
int i;
a=sqrt(n);
b=(int)a;
c=(int)n;
if(c % 2==0)h=0;
if(h==1){
for(i=3;i<=a;i=i+2){
if(c % i==0){
h=0;
break;
}
}
}
return(h);
}
となります。残念ながら、1本化すると、少し速度が落ちるようです。
といって、数%〜1割程度ですが。
6スレッドについてはご自分でお願いします。
これで第22講を終了し、第23講ではBackgroundWorkerによるマルチスレッドに挑戦します。
そして、第24講では新たにFormを派生させるマルチスレッドをご紹介します。
今後の講義予定を書いていて、ひとつ語り落とした問題があることを思い出しました。
『素数で割った余りで分ければ比較的均等にグループ分けできる』という仮説の検証です。
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e)の最後に
w[0]=L"素数個数"; w[1]=(cn1+cn2+cn3+cn4+3).ToString();
dataGridView1->Rows->Add(w);
w[0]=L"1余る";w[1]=cn1.ToString();w[2]=L"2余る";w[3]=cn2.ToString();w[4]=L"3余る";w[5]=cn3.ToString();w[6]=L"3余る";w[7]=cn4.ToString();
dataGridView1->Rows->Add(w);
int min;
min=cn1;
if(cn2<min)min=cn2;
if(cn3<min)min=cn3;
if(cn4<min)min=cn4;
w[0]=L"1余る";w[1]=(((double)cn1/(double)min)).ToString();w[2]=L"1余る";w[3]=(((double)cn2/(double)min)).ToString();
w[4]=L"1余る";w[5]=(((double)cn3/(double)min)).ToString();w[6]=L"1余る";w[7]=(((double)cn4/(double)min)).ToString();
dataGridView1->Rows->Add(w);
}
ピンクを加えて実験し見ると
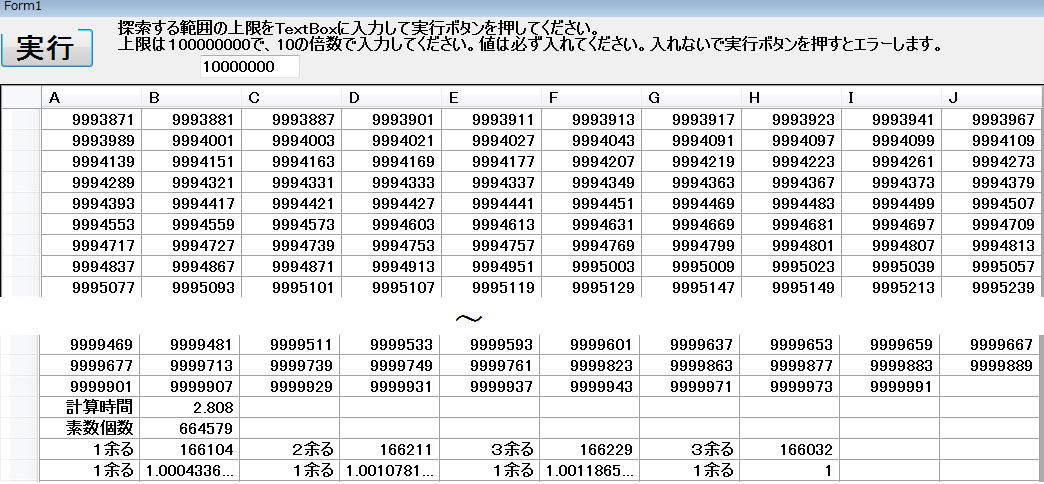
最小の数(min)と最大の数の差は、0.12%しかありませんでした。
すなわち、仮説『素数で割った余りで分ければ比較的均等にグループ分けできる』は検証されたわけです。
というより探索範囲を無限大まで持っていけば『素数で割った余りで分ければ均等にグループ分けできる』という仮説さえ可能です。
