第16講 関数の再帰的呼び出しによる3次・4次魔方陣の作成
第1話 魔方陣や数独はなぜ関数の再帰的呼び出しに向いているのか
さて、予告しておいた通りいよいよ3次と4次の魔方陣に挑戦します。
魔方陣とは、第9講で4次魔方陣と6次魔方陣を作成したとき説明していますが、
再度例を挙げて説明しておきましょう。
3次魔方陣の例
4次魔方陣の例
| 1 |
15 |
12 |
6 |
| 14 |
4 |
7 |
9 |
| 8 |
10 |
13 |
3 |
| 11 |
5 |
2 |
16 |
つまり、すべての行(横)列(縦)対角線の合計が一致する方陣を魔方陣といいます。
第9講においては、分かっている法則をコンピュータに適用しただけなので、
コンピュータが自ら考えて、魔方陣を作ったとは言えません。
しかし、ここでは関数の再帰的呼び出しを利用して、コンピュータ自ら魔方陣をすべて発見させることに挑戦します。
どうして魔方陣の問題は、関数の再帰的呼び出しに向いているのでしょうか。
理由は、各セル(各升=各枠)がもっている同一の性質です。
対角線上のセルを別にすれば、各セルには整数が入り、他のセルとその整数が重なってはいけない、
そして、その列とその行の合計を同じものにしなければならない、要求が課されます。
各セルが持っている条件は同一です。
つまり各セルが持っている性質=構造は同一だということです。
対角線上のセルについては、その基本性質に対角線の合計を同じにせよの条件が付加されるだけです。
このように同じことの繰り返しをする場合は、関数の再帰的利用が向いているのです。
関数が自分自身を呼ぶということは、同じ作業を繰り返すことであるからです。
関数の再帰的呼び出しは、ロシアの入れ子式人形と似ています。
中に同一の構造をもった人形が入っていて、それが繰り返されます。
0番目のセルでやった操作を1番目のセルについても繰り返し、さらに、3番目4番目と繰り返していきます。
同じ操作を繰り返すのですから、関数の再帰的使用が向いているのです。
基本的に第15講で学んだ順列の作成と魔方陣の作成は同じです。
というのは順列の場合は枠(セル)番号が直線に
並んでいたものを、魔方陣においては枠(セル)番号を2次元に配列し直せばよいです。
それに加えて、数字が重複してはいけないというルールも共通です。
したがって、順列を2次元に配置し直して、その中で条件に合う順列を探し出せばよいのです。
条件とは、もちろんすべての列・すべての行・すべての対角線の合計が同一になるということでした。
数独は順列とは異なりますが、各升(セル)の条件はすべて同一です。したがって、各セルは同一構造を持っているのです。
同一構造という言い方が難しいと感じられるなら、同一性質と言い換えてもらっても結構です。
問題はf(g)のgは1次元の枠(セル)番号でした。
このgはいかにしたら2次元に配置し直せるのでしょうか。
第8講ポイントと配列の学習の第5話 2次元配列と1次元配列の関係を参考にして皆さんお考えになって下さい。
Form1は、第15講の後ろから3話を参考に、
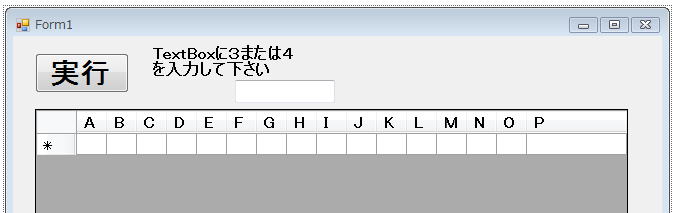 としておきましょう。
としておきましょう。
とりあえずは、3次と4次だけなので15列は使いませんが、将来は14次魔方陣などにも挑戦しますので、
列数は大きめにとっておきましょう。
例えば、3を入れて実行ボタンを押すと
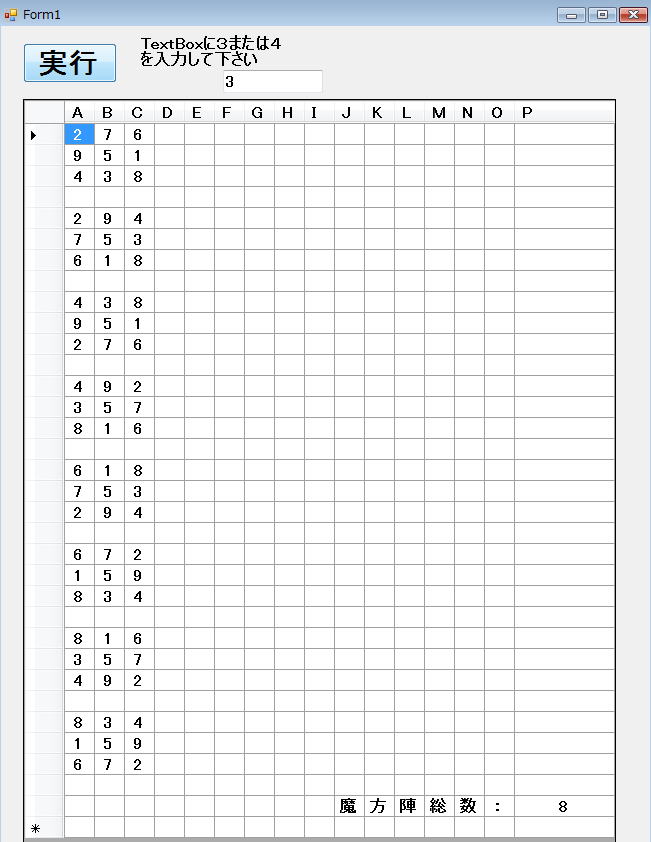 となるように頑張って下さい。
となるように頑張って下さい。
第11講第6話へ 第12講第1話へ 第14講第10話へ 第15講第10話へ 第16講第2話へ

VC++講義第1部へ
vb講義へ
VB講義基礎へ
初心者のための世界で一番わかりやすいVisual C++入門基礎講座
初心者のための世界で一番わかりやすいVisual
Basic入門基礎講座
 としておきましょう。
としておきましょう。 となるように頑張って下さい。
となるように頑張って下さい。