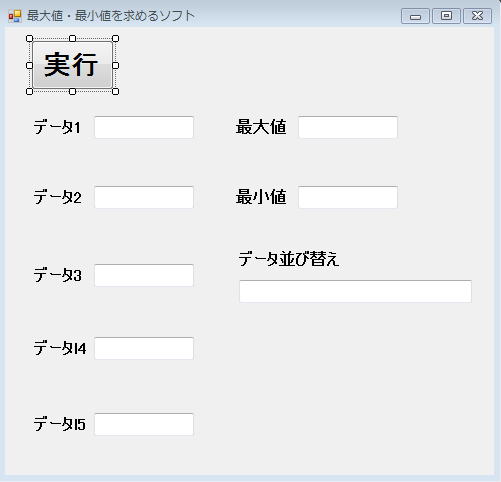
 の場合で作られているので、
の場合で作られているので、データ数が5つの場合のみです。
この実験から分かったことは、データ数が5のときは4ループで並び替えが終わるということです。
実は、次の例を見れば分かる通り、
前回の仮説『n個のデータであれば(n−1)回のループで並び替えは終了する』は、
『n個のデータであれば(n−1)回のループ以内で並び替えは終了する』と訂正しなければならないことが分かります。
データ 85,74,68,55,48
このデータは初めから、大きい順に並んでいます。この場合には、0ループが答えになります。
任意のデータ数で、上の仮説 『n個のデータであれば(n−1)回のループ以内で並び替えは終了する』が実験できるように、
フォームを次のようにいじることにしましょう。
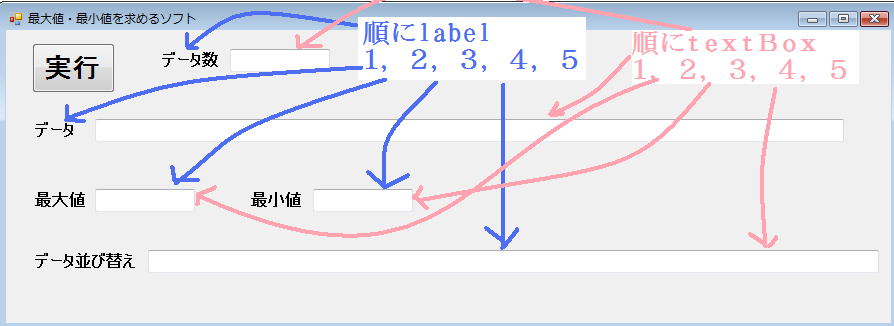 とし、
とし、プログラムソースはピンクの部部を変更したり加えたりします。
#pragma once
#include<stdlib.h>
const int N=30;
namespace o {
・
・
・
#pragma endregion
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
int a[N];
int n=int::Parse(textBox1->Text);
ds(a,n);
Mx(a,n);
Mn(a,n);
Nb(a,n);
}
void Nb(int* p,int n){
char i,j;
int w,cn;
for(i=0;i<n-1;i++){
cn=0;
for(j=0;j<n-1;j++){
if(p[j]<p[j+1]){
w=p[j];
p[j]=p[j+1];
p[j+1]=w;
cn++;
}
}
if(cn==0)break;
}
String^ v=L"";
for(i=0;i<n;i++) v+=(p[i]).ToString()+L" ";
textBox5->Text=v;
}
void ds(int* p,int n){
int i;
String^ w=L"";
for(i=0;i<n;i++){
p[i]=rand() % 100;
w+=(p[i]).ToString()+L" ";
}
textBox2->Text=w;
}
void Mx(int* p,int n){
int i;
int Max=0;
for(i=0;i<n;i++){
if(p[i]>Max){
Max=p[i];
}
}
textBox3->Text=Max.ToString();
}
void Mn(int* p,int n){
int i;
int Min=100;
for(i=0;i<n;i++){
if(p[i]<Min){
Min=p[i];
}
}
textBox4->Text=Min.ToString();
}
};
}
(コピーペースト用
#pragma endregion
private: System::Void button1_Click(System::Object^ sender, System::EventArgs^ e) {
int a[N];
int n=int::Parse(textBox1->Text);
ds(a,n);
Mx(a,n);
Mn(a,n);
Nb(a,n);
}
void Nb(int* p,int n){
char i,j;
int w,cn;
for(i=0;i<n-1;i++){
cn=0;
for(j=0;j<n-1;j++){
if(p[j]<p[j+1]){
w=p[j];
p[j]=p[j+1];
p[j+1]=w;
cn++;
}
}
if(cn==0)break;
}
String^ v=L"";
for(i=0;i<n;i++) v+=(p[i]).ToString()+L" ";
textBox5->Text=v;
}
void ds(int* p,int n){
int i;
String^ w=L"";
for(i=0;i<n;i++){
p[i]=rand() % 100;
w+=(p[i]).ToString()+L" ";
}
textBox2->Text=w;
}
void Mx(int* p,int n){
int i;
int Max=0;
for(i=0;i<n;i++){
if(p[i]>Max){
Max=p[i];
}
}
textBox3->Text=Max.ToString();
}
void Mn(int* p,int n){
int i;
int Min=100;
for(i=0;i<n;i++){
if(p[i]<Min){
Min=p[i];
}
}
textBox4->Text=Min.ToString();
}
};
}
)
F5を押して、実行してデータ数の中に30以下のデータを入れて何度実験してもうまくいくことが分かります。
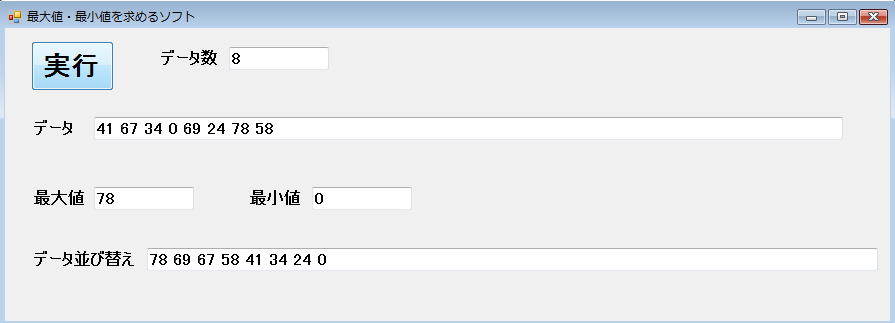
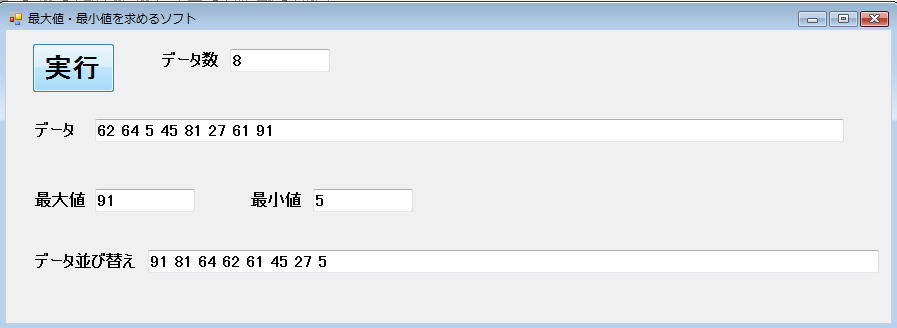

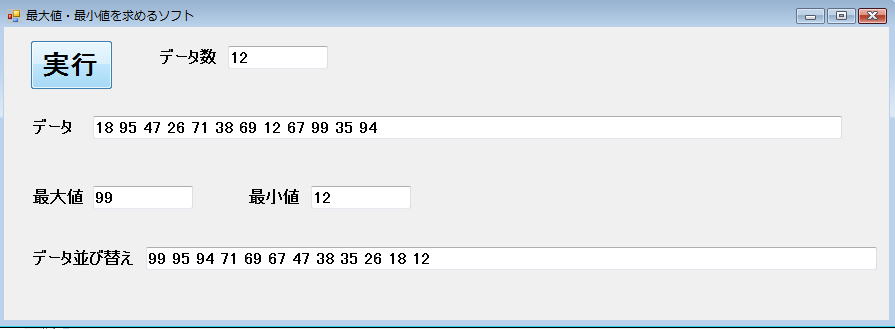
というわけで、先の仮説『n個のデータであれば(n−1)回のループ以内で並び替えは終了する』は証明されたわけです。
といっても数学的に証明されたわけではなく、実験的に証明されただけです。
プログラムは必ずしも数学的に証明されたものだけを扱うわけではありません。
例えば、将棋ソフトを考えれば分かります。
当然必勝法は、数学的には証明されておりません。
でもできるだけ、正しい手を指すように、できるだけ強くなるようにプログラマーは工夫するだけです。
作ったソフトが強いかどうかは、当然数学的には証明することはできず、
実際に人間や他のソフトと対戦させて、実験するしかありません。
現在最強のソフトはおそらくアマチュア6,7段程度でしょうか。
しかし、近い将来プロの名人に勝つようになるでしょう。
将棋ソフトの歴史は、日進月歩だからです。
先の仮説『n個のデータであれば(n−1)回のループ以内で並び替えは終了する』はもちろん数学的に証明するのは可能でしょう。
ですが、証明しようとすればかなり難しい証明になるでしょう。
尚、if(cn==0)break;は並び替えが終了している場合に、ループ文を抜けるように入れました。
では、皆さん私が考えた2つの方法以外に並び替えの方法を考えてプログラミングしてみてください。
尚、この第12講は後いくつか並び替えの方法を考えてから、
最後にライブラリにあるsetとsortを紹介する予定になっています。
