マルチスレッド版数独自動生成ソフトC++コードを題材とする超初心者のためのVisual Studio C++講義
第６章 ６次魔方陣・８次魔方陣の作成

第１話 偶数魔方陣の一般的作成方法


前話で話した通り、私は作成という言葉と生成という言葉を区別して使っています。

作成は人間がコンピュータに作り方を教えるだけですから、

400次魔方陣でもあっという間（おそらく、0.01秒未満）に作り出してしまいます。

それに対して自動生成の場合には、

コンピュータが自ら考えて魔方陣を作り出すので現在のパソコンの性能を使っても、

精々20次魔方陣が限界だと思われます。

ただし、それは私のぼんくらな頭を前提する場合であって、

皆さんの中にはとんでもない才能の持ち主がいて、

20次の壁をあっさり破って50次辺りでも余裕で生成させるかもしれません。

ここでついてきた小学生や中学生なら間違いなく天才であり、

私を遥かに超えるプログラマーになるでしょう。


さて、本題に入りましょう。

この講義のトップページに書いてある通り、

小学生・中学生のための魔方陣授業

をぜひ参照してください。

特に、
第２５回　自然配列から魔方陣へ（偶数次魔方陣の一般的作成方法）第１弾
第２６回　自然配列から魔方陣へ（偶数次魔方陣の一般的作成方法）第２弾
第２７回　自然配列から魔方陣へ（偶数次魔方陣の一般的作成方法）第３弾
第２８回　新魔方陣の法則（偶数次版魔方陣の法則）第１弾
第２９回　新魔方陣の法則（偶数次版魔方陣の法則）第２弾
辺りを参照してほしいのですが、

ここでも簡単に復習しておきます。

６次魔方陣の場合

1 2 3 4 5 6
7 8 9 10 11 12
13 14 15 16 17 18
19 20 21 22 23 24
25 26 27 28 29 30
31 32 33 34 35 36


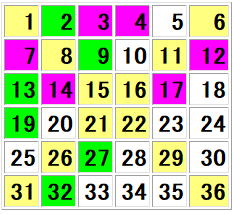（同じもの図にしました）

４次魔方陣に比べればかなり複雑になりますが、

黄色（など）の対角線のセル（ます）は中央の点に対して点対称移動をします。

明るい紫は中央の直線に対して左右に線対称移動をします。

緑は中央の線に対して上下に線対称移動をします。

すると、

36 2 3 4 5 31
7 29 9 10 26 12
13 14 22 21 17 18
19 20 16 15 23 24
25 11 27 28 8 30
6 32 33 34 35 1


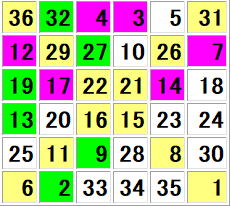（同じもの図にしました）

こちらも同じくすべての行合計・すべての列合計・すべての対角線合計を計算して

すべてが (1 + 2 + 3 +・・・ +36) ÷ 6 = 111 になっていることを確認してください。

８次魔方陣も同じです。

1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
25 26 27 28 29 30 31 32
33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48
49 50 51 52 53 54 55 56
57 58 59 60 61 62 63 64


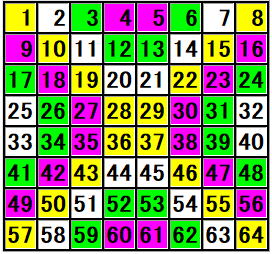（同じもの図にしました）


黄色（など）の対角線のセル（ます）は中央の点に対して点対称移動をします。

明るい紫は中央の直線に対して左右に線対称移動をします。

緑は中央の線に対して上下に線対称移動をします。

すると、

1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
25 26 27 28 29 30 31 32
33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48
49 50 51 52 53 54 55 56
57 58 59 60 61 62 63 64


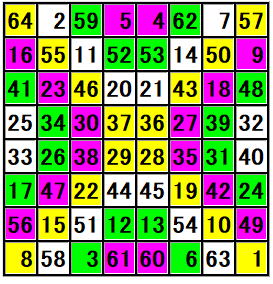（同じものを図にしました）
皆さん、すべての行合計・すべての列合計・すべての対角線合計を計算して

すべてが (1 + 2 + 3 +・・・ + 64) ÷ 8 = 260 になっていることを確認してください。

※1〜36 の合計は 36×37÷2 = 666、
魔方陣の1行の合計は 666÷6 = 111 になります。

※1〜64 の合計は 64×65÷2 = 2080、
魔方陣の1行の合計は 2080÷8 = 260 になります。






第５章第12話へ　第６章第２話へ

本講義トップへ