第5章 配列
第12話 対角線合計を計算して表示する
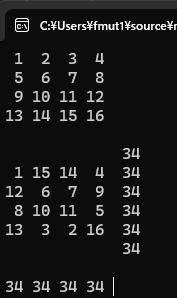
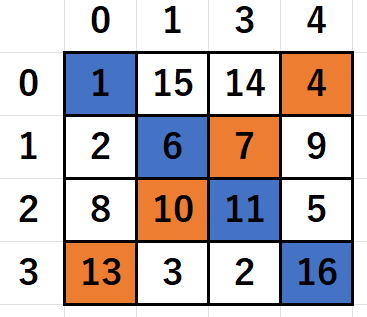
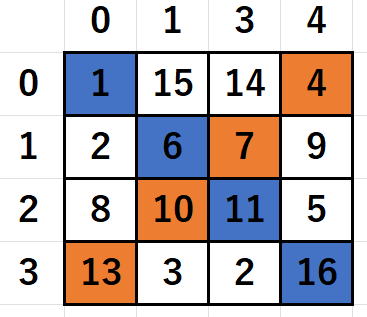
(
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
34
1 15 14 4 34
12 6 7 9 34
8 10 11 5 34
13 3 2 16 34
34
34 34 34 34
)
列合計計算と表示を実現するコード例
#include<iostream>//インクルードファイルiostreamの読み込み
#include<conio.h>//while(!_kbhit());を使うためのお呪い
#include<string> //文字列変数を使えるようにするために組み込む
#include <iomanip> //setprecisionを使えるように組み込む
#include <cmath>//powなどを使うときに必要
#include <ctime>//time()(←現時刻発生する関数)を使うために必要
using namespace std;//coutを使うときに必要なお呪い
void 2次元for文();//横と縦の2方向を持つ2次元for文体験
int main() {//私は社長だ。
2次元for文();
while (!_kbhit());//待機させるための命令
return(0);//int main()終わるためのお呪い
}
void 2次元for文() {
//横と縦の2方向を持つ2次元for文体験
int a[4][4];//4行4列の行列を表すことのできる2次元配列の宣言
for (int i = 0; i < 4; i++) {
for (int j = 0; j < 4; j++) {
a[i][j] = 4 * i + j + 1;
}
}
for (int i = 0; i < 4; i++) {
for (int j = 0; j < 4; j++) {
if (a[i][j] < 10)cout << " ";
cout << a[i][j] << " ";
}
cout << endl;
}
//以下
//a[0][1]とa[3][2]の交換
//a[0][2]とa[3][1]の交換
//a[1][0]とa[2][3]の交換
//a[2][0]とa[1][3]の交換
int 受け皿;//a[0][1]などのデータを一時的に預かる変数
//a[0][1]とa[3][2]の交換
受け皿 = a[0][1];//a[0][1]のデータを上書きする前に 受け皿 に一時的にデータを預ける
a[0][1] = a[3][2];
//a[0][1]のデータがa[3][2]のデータに上書きされてしまうが、値は 受け皿 に残っている
a[3][2] = 受け皿;
//a[0][1]の元のデータをa[3][2]に入力
//a[0][1]とa[3][2]の交換終了
//a[0][2]とa[3][1]の交換
受け皿 = a[0][2];//a[0][2]のデータを上書きする前に 受け皿 に一時的にデータを預ける
a[0][2] = a[3][1];
//a[0][2]のデータがa[3][1]のデータに上書きされてしまうが、値は 受け皿 に残っている
a[3][1] = 受け皿;
//a[0][2]の元のデータをa[3][1]に入力
//a[0][2]とa[3][1]の交換終了
//a[1][0]とa[2][3]の交換
受け皿 = a[1][0];//a[0][1]のデータを上書きする前に 受け皿 に一時的にデータを預ける
a[1][0] = a[2][3];
//a[1][0]のデータがa[2][3]のデータに上書きされてしまうが、値は 受け皿 に残っている
a[2][3] = 受け皿;
//a[1][0]の元のデータをa[3][2]に入力
//a[0][1]とa[2][3]の交換終了
//a[2][0]とa[1][3]の交換
受け皿 = a[2][0];//a[2][0]のデータを上書きする前に 受け皿 に一時的にデータを預ける
a[2][0] = a[1][3];
//a[2][0]のデータがa[1][3]のデータに上書きされてしまうが、値は 受け皿 に残っている
a[1][3] = 受け皿;
//a[2][0]の元のデータをa[1][3]に入力
//a[2][0]とa[1][3]の交換終了
int 行合計[4] = { 0,0,0,0 };
//各行の合計を出す配列を定義して、すべてを0に初期化
//各行の合計を計算する
for (int i = 0; i < 4; i++) {
for(int j = 0; j < 4; j++) {
行合計[i] = 行合計[i] + a[i][j];
}
}
int 列合計[4] = { 0,0,0,0 };
//各行の合計を出す配列を定義して、すべてを0に初期化
//各行の合計を計算する
for (int i = 0; i < 4; i++) {
for (int j = 0; j < 4; j++) {
列合計[i] = 列合計[i] + a[j][i];
}
}
cout << endl;
//対角線合計計算と表示
int 対角線合計[2] = { 0,0 };//1次元配列を対角線合計定義してすべての値を0に初期化
//対角線合計の計算
for (int i = 0; i < 4; i++) {
対角線合計[0] = 対角線合計[0] + a[i][i];
}
//対角線合計の表示
for (int i = 0; i < 4; i++) {
cout << " ";
}
cout << " " << 対角線合計[0];
//逆対角線合計の計算
for (int i = 0; i < 4; i++) {
対角線合計[1] = 対角線合計[1] + a[i][3 - i];
}
cout << endl;
for (int i = 0; i < 4; i++) {
for (int j = 0; j < 4; j++) {
if (a[i][j] < 10)cout << " ";
cout << a[i][j] << " ";
}
cout << " " << 行合計[i];
cout << endl;
}
//逆対角線合計の表示
for (int i = 0; i < 4; i++) {
cout << " ";
}
cout << " " << 対角線合計[1] << endl;
//各列の合計を表示
cout << endl;
for (int i = 0; i < 4; i++) {
cout << 列合計[i] << " ";
}
}
これで行・列・対角線のすべての合計が計算できるようになりました。
//対角線合計の計算
for (int i = 0; i < 4; i++) {
対角線合計[0] = 対角線合計[0] + a[i][i];
}
と
//逆対角線合計の計算
for (int i = 0; i < 4; i++) {
対角線合計[1] = 対角線合計[1] + a[i][3 - i];
}
は初心者の方には難しいと思いますので、
解説します。