④![]() は解を一つ持つとき、解は無数に存在するか。
は解を一つ持つとき、解は無数に存在するか。
まず具体的な場合で考えてみよう。
![]() A
A
は解(x,y,z)=(1,1,3)をもっている。このときわれわれが定義する意味で、異なる解を無数に持っているであろうか。われわれの定義で、二つの解![]() ,
,![]() が異なる条件は
が異なる条件は
![]()
であった。
式Aの両辺を![]() で割り、
で割り、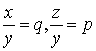 と置くと、
と置くと、
![]() B
B
双曲線上Bに有理点(p,q)=(3,1)が存在している。そこで、点(3,1)を通る直線の傾きをtとすると、
![]() C
C
式Bに代入して整理すると、
![]()
解の一つは、p=3である。よって、他の解をβとすると、2次方程式のおける解と係数の関係から、
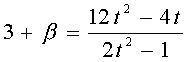
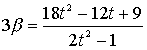
であるがいずれの場合も、
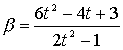
よって、tが有理数であればβは有理数である。
βをpと置き直して。
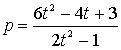
式Cに代入して、
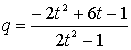
tは任意の有理数をとることができるから、方程式Bは解
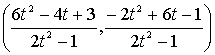
を無数に持っていることが証明された。
t=1のとき、
(p,q)=(5,3)
このとき、方程式Aの解は
(x,y,z)=(3,1,5)
t=2のとき、
(p,q)=(19/7,3/7)
(x,y,z)=(3,7,19)
t=3/4のとき、
(p,q)=(27,19)
(x,y,z)=(19,1,27)
t=4/5のとき、
(p,q)=(13,9)
(x,y,z)=(9,1,13)
t=8/11のとき、
(p,q)=(395/7,279/7)
(x,y,z)=(279,7,395)
次に一般的に考えてみよう。
![]() B
B
に解![]() が存在すると仮定しよう。
が存在すると仮定しよう。
![]() D
D
前と同様に点![]() を通り、傾きがtの直線を考えると、
を通り、傾きがtの直線を考えると、
![]() E
E
式Bに代入して整理すると、
![]()
一方の解は![]() なので、他方の解をβとすれば解と係数の関係から
なので、他方の解をβとすれば解と係数の関係から
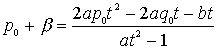 F
F
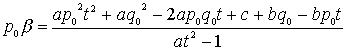 G
G
式Fから
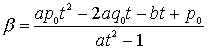
式Gから
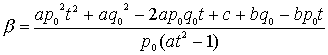
これに式Dを代入すれば
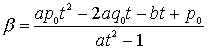
よって、式EからもFからも同じものが導かれる。
(ここでは解と係数の関係で解いたが、2次方程式の解の公式に代入しても解ける。そのさい、魔法のようにルートが消えてしまうことを、読者自身で確認していただきたい。)
tが有理数であれば、βは有理数。
よって、任意の有理数tについて、
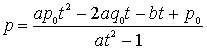
は方程式![]() の
の![]() 以外の解であり、無数に存在することがわかる。式Eに代入して、
以外の解であり、無数に存在することがわかる。式Eに代入して、
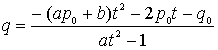
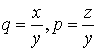 より、
より、
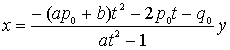
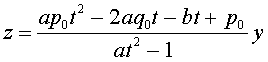
よって、任意の有理数t、yに対して、
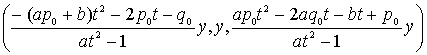
は![]() の有理数解である。そして、分母の公倍数をかけるなら自然数解となる。
の有理数解である。そして、分母の公倍数をかけるなら自然数解となる。
以上から、方程式![]() は有理数解を一つ持つなら、有理数解(分母の公倍数かけるなら自然数解)を無数に持っていることが証明された。よって、方程式
は有理数解を一つ持つなら、有理数解(分母の公倍数かけるなら自然数解)を無数に持っていることが証明された。よって、方程式![]() は自然数解を無数に持つか、一つも持たないかのどちらかであるという拡大フェルマー予想は、2次では証明されたことになる。
は自然数解を無数に持つか、一つも持たないかのどちらかであるという拡大フェルマー予想は、2次では証明されたことになる。
